Next: 統計的推定法 Up: 確率分布 Previous: 連続型確率分布(continuous probability distribution) 目次 索引
確率変数 の確率密度関数が
の確率密度関数が
![$\displaystyle g(x) = \frac{1}{\sqrt{2\pi} \sigma} EXP\left[-\frac{(x-\mu)^2}{2 \sigma^2}\right], \ -\infty < x < \infty $](img206.png)
 は正規分布に従うといい,
は正規分布に従うといい,
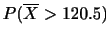 と表わします.
と表わします.
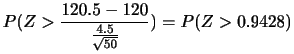 を表すと,次のようになります.
を表すと,次のようになります.
![\includegraphics[width=14.5cm]{STATFIG/Fig2-1-1.eps}](img209.png)
このままでは,比較しにくいので,標準化(normalization)を行ないます.
標準化
確率変数 の平均
の平均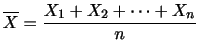 を0に,分散
を0に,分散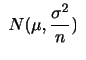 を1に直すことを標準化といいます.
を1に直すことを標準化といいます.
標準化の方法
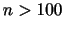
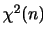
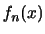 を求めるには,
を求めるには,
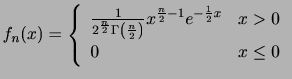 を求めます.
を求めます.
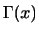 は標準正規分布の左半分なので,その値は0.5となります.
は標準正規分布の左半分なので,その値は0.5となります.
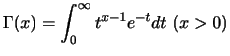 の値は標準正規分布表を用いて求めます.
の値は標準正規分布表を用いて求めます.
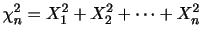 のとき,
のとき,
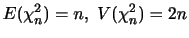 を求めよ
を求めよ
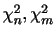 を求めよ.
を求めよ.
解答
(1) 標準化を行うと,
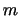 |
 |
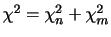 |
|
 |
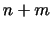 |
||
 |
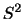 |
(2)
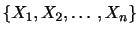 |
|||
 |
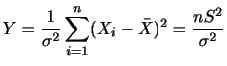 |
||
 |
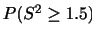 |
||
 |
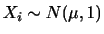 |
||
 |
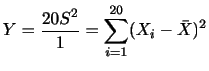 |
|
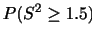 のとき,次の確率を求めよ.
のとき,次の確率を求めよ.
2. 都市Aの夏期を除く各期の一人一日当たりの水需要量は,これまでの何年かの実績からほぼ
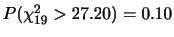 に従うことが分かっているとする.今年の一人当たりの水需要量(夏期を除く)が250(l/人)以上になる確率を求めよ.
に従うことが分かっているとする.今年の一人当たりの水需要量(夏期を除く)が250(l/人)以上になる確率を求めよ.