Next: 索引 Up: 統計学入門 Previous: 検定に用いる統計量(test statistics) 目次 索引
階級数
 また最大値440最小値300より,階級幅は
また最大値440最小値300より,階級幅は
階級幅
 となるので,階級幅を18ととることにします.これより度数分布表を作成します.
となるので,階級幅を18ととることにします.これより度数分布表を作成します.
平均値
 |
 |
![$\displaystyle \frac{1}{100}[318\cdot2 + 336\cdot 10 + 354\cdot 25 + 363 \cdot 31 + 381 \cdot 8 + 399 \cdot 18 + 417 \cdot 5 + 435 \cdot 1]$](img728.png) |
|
 |
 |
最大値 440
最小値 300
中央値

最頻値 363
電卓を使う場合は必ず途中の値を書く必要があります.また,計算は小数点以下2桁までで表わすことにします.






これより
 |
 |
 |
|
 |
 |

階級数

また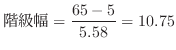 の最大値109最小値13より
の最大値109最小値13より
階級幅

これより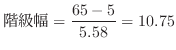 の階級幅を17と取ります.また
の階級幅を17と取ります.また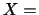 の最大値65最小値5より
の最大値65最小値5より

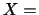 の階級幅を10と取ります.
の階級幅を10と取ります.






 |
 |
 |
|
 |
 |

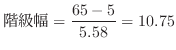 上の
上の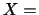 の回帰直線は
の回帰直線は


1.
 |
 |
 |
|
 |
 |
 |
 |
 |
|
 |
 |
(2)  を一人一日当たりの水需要量とすると,
を一人一日当たりの水需要量とすると,
 .これより一人当たりの水需要量(夏期を除く)が250(l/人)以上になる確率は
.これより一人当たりの水需要量(夏期を除く)が250(l/人)以上になる確率は
 で与えられる.したがって,
で与えられる.したがって,
 |
 |
 |
|
 |
 |
 |
 |
 |
|
 |
 |
 |
|
 |
 |
 より,
より, となります.
となります.
1 ある水域の一定区間における水質BODを とおくと,
とおくと,
 .又,標本数は15で,標本平均
.又,標本数は15で,標本平均
 より,
より,

 を標準化すると,
を標準化すると,


 を標準正規分布表を用いて求めると,
を標準正規分布表を用いて求めると,
 したがって,95%信頼区間は
したがって,95%信頼区間は


2 標準偏差が2.5より,母分散
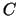 は既知である.この母集団から無作為に選んだ標本
は既知である.この母集団から無作為に選んだ標本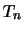 は
は
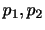 の正規分布に従っていると考えることができる.したがって,
の正規分布に従っていると考えることができる.したがって,
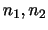
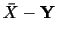 を求めると,
を求めると,
![$\displaystyle \bar{X} = \frac{1}{4}[145.3 + 145.1 + 145.4 + 146.2] = \frac{582}{4} = 145.5$](img776.png)

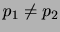 . また,
. また,
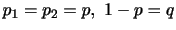 . したがって,
. したがって,



3 母平均 であるが母分散
であるが母分散
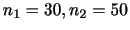 は未知である.この母集団から無作為に選んだ標本
は未知である.この母集団から無作為に選んだ標本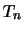 は
は
 の正規分布に従っていると考えることができる.したがって,
の正規分布に従っていると考えることができる.したがって,

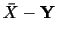 を求めると,
を求めると,
![$\displaystyle \bar{X} = \frac{1}{4}[145.3 + 145.1 + 145.4 + 146.2] = \frac{582}{4} = 145.5$](img776.png)
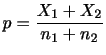 を用いると,
を用いると,

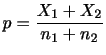 を求めると,
を求めると,
 |
 |
![$\displaystyle \frac{1}{3}[(145.3 - 145.5)^{2} + (145.1 - 145.5)^{2} + (145.4 - 145.5)^{2} + (146.2 - 145.5)^{2}]$](img786.png) |
|
 |
 |
95%信頼区間より,
 . また,
. また,
 . したがって,
. したがって,



1 標本比率は
 .また,
.また,
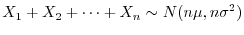 であるから,十分大きな
であるから,十分大きな に対して,統計量
に対して,統計量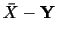 の分布が正規分布
の分布が正規分布
 で近似される.したがって,与えられた
で近似される.したがって,与えられた に対して
に対して


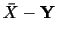 と
と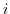 を
を で置き換えると,
で置き換えると,


 となる.
となる.
1 標本比率は
 .また,
.また,
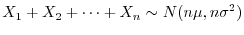 であるから,十分大きな
であるから,十分大きな に対して,統計量
に対して,統計量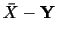 の分布が正規分布
の分布が正規分布
 で近似される.したがって,与えられた
で近似される.したがって,与えられた に対して
に対して


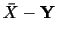 と
と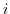 を
を で置き換えると,
で置き換えると,


 となる.
となる.
1 この工場の製品を とすると,
とすると,
 であることが分かる.この工場から16個の製品を取り出したとき,
であることが分かる.この工場から16個の製品を取り出したとき,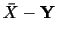 をそれらの標本平均とすると,
をそれらの標本平均とすると,

1
 |
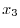 |
 |
|
 |
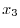 |
 |
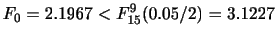
3 統計量 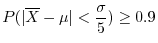 が既知より,
が既知より,

 のもとで,
のもとで,

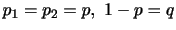 より,
より, を容認する.
を容認する.
95%信頼区間は


2 この工場の製品を とすると,
とすると,
 であることが分かる.この工場から8個の製品を取り出したとき,
であることが分かる.この工場から8個の製品を取り出したとき,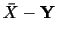 をそれらの標本平均とすると,
をそれらの標本平均とすると,

1
 |
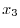 |
 |
|
 |
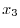 |
 |
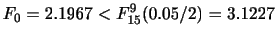
3 統計量 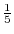 が既知で
が既知で
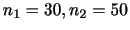 の検定を行なうので
の検定を行なうので

 のもとで
のもとで
![$\displaystyle S^{2} = \frac{1}{8}[(11.97-12.02)^{2} + \cdots + (12.05 - 12.028)^{2}] = 0.0021$](img818.png)


 は棄却される.
は棄却される.
95%信頼区間は



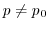 |
 |
 |
|
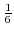 |
 |
 |
母平均の差の検定である.
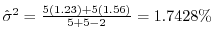 より,
より,
1
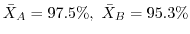
2 有意水準
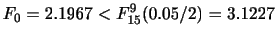
3 統計量


4  のもとで,
のもとで,

5
 より,
より,

 は棄却されない.
は棄却されない.
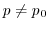 |
 |
 |
|
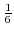 |
 |
 |
母分散の比の左側検定である.

1

2 有意水準
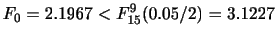
3 統計量

4  のもとで,
のもとで,

5


 は棄却されない.
は棄却されない.
一般に,

1
現在の政党支持率を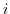 とする.
とする.
 : 「政党支持率は変わらない」
: 「政党支持率は変わらない」
 : 「政党支持率は変わった」
: 「政党支持率は変わった」

2 有意水準
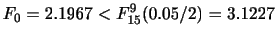
3 統計量 標本数が3000と大標本の場合と考えられるので,標本比率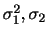 は近似的に正規分布
は近似的に正規分布
 に従う.よって,標準化を行うと
に従う.よって,標準化を行うと
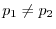
4  のもとで,
のもとで,
 より,
より,

5

 を容認できない.
を容認できない.
1
ある番組を好きな男性の割合を ,女性が好きな割合を
,女性が好きな割合を とする.
とする.
 : 「視聴率に男女差はない」
: 「視聴率に男女差はない」 
 : 「視聴率に男女差はある」
: 「視聴率に男女差はある」

2 有意水準
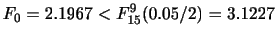
3 母比率の差の検定より,

4  のもとで,
のもとで,
 . よって
. よって

5

 の視聴率に男女差はないを容認
の視聴率に男女差はないを容認
1
 : 「メンデル比に従っている」
: 「メンデル比に従っている」

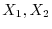 : 「メンデル比に従っていない」
: 「メンデル比に従っていない」

2 有意水準
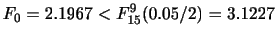
3 統計量

4  のもとで,
のもとで,
 |
 |
 |
|
 |
 |
5
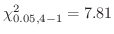 より,
より,
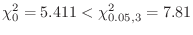
 を容認.
を容認.
1
 : 「ポワソン分布
: 「ポワソン分布
 に従っている」
に従っている」
2 有意水準
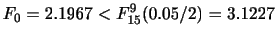
3 統計量
この表をポワソン分布とみて,死亡数の理論値を求める.これがポワソン分布
 によるものと考えて,
によるものと考えて, の値を推定する.死亡者数
の値を推定する.死亡者数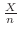 のときの確率を
のときの確率を とすると,
とすると,

| 死亡者数 | 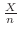 |
0 | 1 | 2 | 3 | 4 | 計 |
| 部隊数 | 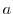 |
142 | 99 | 46 | 11 | 2 | 300 |
 |
0 | 99 | 92 | 33 | 8 | 232 | |
 |
0.473 | 0.33 | 0.153 | 0.036 | 0.0066 | ||
| 理論度数 |  |
141.9 | 99 | 45.9 | 10.8 | 1.98 |
 より
より
 .これより平均値
.これより平均値 は
は
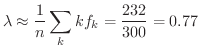
| 死亡者数 | 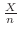 |
0 | 1 | 2 | 3 | 4 | 計 |
| 部隊数 | 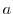 |
142 | 99 | 46 | 11 | 2 | 300 |
| 理論度数 |  |
141.9 | 99 | 45.9 | 10.8 | 1.98 |
この表で,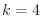 の所の
の所の は単独で5よりも小さいので,
は単独で5よりも小さいので, 検定ができない.そこで,右から順に
検定ができない.そこで,右から順に を加えて5を越すまで合併すると,
を加えて5を越すまで合併すると, の階級を1つにしなければならない.したがって,
の階級を1つにしなければならない.したがって,
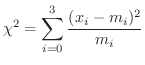
4  のもとで,
のもとで,
 |
 |
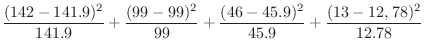 |
|
 |
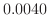 |
5
 より,
より,
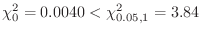
 を容認.
を容認.
母数 が標本から1個推定されたので,自由度は
が標本から1個推定されたので,自由度は
 となる.
となる.
1
 : 「飲酒と喫煙とは独立である.」
: 「飲酒と喫煙とは独立である.」
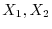 : 「飲酒と禁煙とは独立ではない.」
: 「飲酒と禁煙とは独立ではない.」
2 有意水準
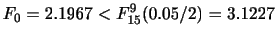
3 統計量
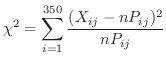
4  のもとで,
のもとで,
 |
 |
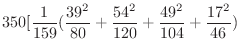 |
|
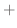 |
![$\displaystyle \frac{1}{119}(\frac{27^{2}}{80} + \frac{43^{2}}{120} + \frac{40^{...
...14^{2}}{80} + \frac{23^{2}}{120} + \frac{15^{2}}{104} + \frac{20^{2}}{46})] - 1$](img873.png) |
||
 |
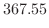 |
4 自由度
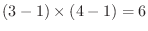 より,
より,
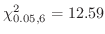 .
.
5
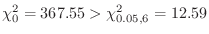 より,
より, は棄却される.したがって,飲酒と喫煙には関係がある.
は棄却される.したがって,飲酒と喫煙には関係がある.