next up previous contents
Next: Multidimensional probability distribution Up: Random variables Previous: Two-dimensional probability distribution   Contents

Mean and variance of random variables

Exercise 6

1. For $f(x) = \left\{\begin{array}{ll} 1 - \vert x\vert & (-1 \leq x \leq 1)\\ 0 & (\mbox{other}) \end{array}\right. $
answer the following questions.

(a)
Show that $f(x)$ is a probability density function.
(b)
Find the distribute function $F(x)$．
(c)
Find $P_{r}(-\frac{1}{2} \leq X \leq \frac{1}{2})$．
(d)
Find $E(X), V(X)$．

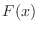2. When throwing one dice three times, the number of times a 1 is rolled is 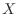$X$．Then

(a)
find the probability distribution of $X$.
(b)
find the expectation and the standard deviation of $X$．
(c)
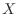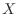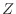Find the random variable $Z$, which is a standardized version of 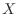$X$，Furthermore, find the probability distribution of $Z$.．

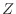3. Find the probability of the followings using Bernoulli's theorem．

(a)
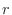When one coin is thrown 1000 times, let $r$ be the number of times the head appears. Then find the probability that

$\displaystyle \left\vert\frac{r}{1000} - \frac{1}{2}\right\vert < \frac{1}{10} $

(b)
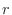When two coins are thrown 1000 times, let $r$ be the number of times the head appears on both coins. Then find the probability that

$\displaystyle \left\vert\frac{r}{1000} - \frac{1}{4}\right\vert < \frac{1}{10} $

(c)
Throw one coin 2000 times and find the probability that the number of heads coming out is less than 50 times from 1000 times．
(d)
How many times do we have to throw a coin if after throwing one coin 2000 times, the probability that the difference between the head output rate and the theoretical probability of $0.5$ is within $5\%$ is $99 \%$ or more.

Answer

(1)

a

$\displaystyle 1 - \vert x\vert = \left\{\begin{array}{cl} 1 + x & -1 < x < 0\\ 1 - x & 0 < x < 1 \end{array} \right. $

implies $f(x)\geq 0$．Also
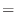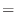$\displaystyle \int_{-\infty}^{\infty} f(x) dx$ $\displaystyle =$ $\displaystyle \int_{-\infty}^{-1} 0dt + \int_{-1}^{0} (1 + t)dt + \int_{0}^{1} (1-t)dt + \int_{1}^{\infty} 0 dt$  
  $\displaystyle =$ $\displaystyle \left[t + \frac{t^2}{2}\right]_{-1}^{0} + \left[t - \frac{t^2}{2}\right]_{0}^{1}$  
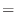  $\displaystyle =$ $\displaystyle -(-1 + \frac{1}{2}) + 1 - \frac{1}{2} = 1$  

b

For $x < -1$,

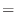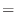$\displaystyle F(x) = P_{r}(X \leq x) = \int_{-\infty}^{0} 0dt = 0 $

For $-1 < x < 0$,
$\displaystyle F(x) = P_{r}(X \leq x) = \int_{-\infty}^{x} f(t) dt $ $\displaystyle =$ $\displaystyle \int_{-\infty}^{-1} 0dt + \int_{-1}^{x} (1 + t)dt$  
  $\displaystyle =$ $\displaystyle \left[t + \frac{t^2}{2}\right]_{-1}^{x}$  
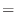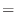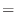  $\displaystyle =$ $\displaystyle x + \frac{x^2}{2} -(-1 + \frac{1}{2}) = \frac{1}{2}(x+1)^2$  

For $0 < x < 1$,，
$\displaystyle F(x) = P_{r}(X \leq x) = \int_{-\infty}^{\infty} f(x) dx$ $\displaystyle =$ $\displaystyle \int_{-\infty}^{-1} 0dt + \int_{-1}^{0} (1 + t)dt + \int_{0}^{x} (1-t)dt$  
  $\displaystyle =$ $\displaystyle \left[t + \frac{t^2}{2}\right]_{-1}^{0} + \left[t - \frac{t^2}{2}\right]_{0}^{x}$  
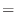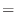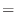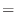  $\displaystyle =$ $\displaystyle -(-1 + \frac{1}{2}) + x - \frac{x^2}{2} = \frac{1}{2} + \frac{x}{2}(2 - x)$  

c

$\displaystyle P_{r}(-\frac{1}{2} < X < \frac{1}{2}) = F(\frac{1}{2}) - F(-\frac... ...}{2} + \frac{1}{4}(2 - \frac{1}{2}) - \frac{1}{2}(\frac{1}{2})^2 = \frac{3}{4} $

d

$\displaystyle E(X)$ $\displaystyle =$ $\displaystyle \int_{-\infty}^{\infty} x f(x) dx$  
  $\displaystyle =$ $\displaystyle \int_{-\infty}^{-1} 0dx + \int_{-1}^{0}x(1+x)dx + \int_{0}^{1}x(1-x)dx + \int_{1}^{\infty} 0dx$  
  $\displaystyle =$ $\displaystyle \left[\frac{x^2}{2} + \frac{x^3}{3}\right]_{-1}^{0} + \left[\frac{x^2}{2} - \frac{x^3}{3}\right]_{0}^{1} = 0$  


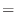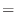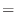$\displaystyle E(X^2)$ $\displaystyle =$ $\displaystyle \int_{-\infty}^{\infty} x^2 f(x) dx$  
  $\displaystyle =$ $\displaystyle \int_{-\infty}^{-1} 0dx + \int_{-1}^{0}x^2(1+x)dx + \int_{0}^{1}x^2(1-x)dx + \int_{1}^{\infty} 0dx$  
  $\displaystyle =$ $\displaystyle \left[\frac{x^3}{3} + \frac{x^4}{4}\right]_{-1}^{0} + \left[\frac{x^3}{3} - \frac{x^4}{4}\right]_{0}^{1}$  
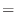  $\displaystyle =$ $\displaystyle -(-\frac{1}{3} + \frac{1}{4}) + \frac{1}{3} - \frac{1}{4} = \frac{2}{3} - \frac{1}{2} = \frac{1}{6}$  

これより

$\displaystyle V(X) = E(X^2) - E(X)^2 = \frac{1}{6} $

2.

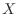a Let $X$ be the number of times 1 is rolled. Then

$\displaystyle P_{r}(X = 0) = \binom{3}{0}\left(\frac{5}{6}\right)^3 = \frac{125}{216}$

$\displaystyle P_{r}(X = 1) = \binom{3}{1}\left(\frac{1}{6}\right)\left(\frac{5}{6}\right)^{2} = \frac{25}{72} $

$\displaystyle P_{r}(X = 2) = \binom{3}{2}\left(\frac{1}{6}\right)^2 \left(\frac{5}{6}\right) = \frac{5}{72} $

$\displaystyle P_{r}(X = 3) = \binom{3}{3}\left(\frac{1}{6}\right)^3 = \frac{1}{216} $

b

$\displaystyle E(X) = \sum_{i=0}^{n} i \cdot P_{r}(X = i) = 0\cdot \frac{125}{21... ...dot \frac{25}{72} + 2 \cdot \frac{5}{72} + 3 \cdot \frac{1}{216} = \frac{1}{2} $

$\displaystyle E(X^2) = \sum_{i=0}^{n} i^2 \cdot P_{r}(X = i) = 0\cdot \frac{125... ...\frac{25}{72} + 2^2 \cdot \frac{5}{72} + 3^2 \cdot \frac{1}{216} = \frac{2}{3} $

$\displaystyle V(X) = E(X^2) - \left(E(X)\right)^2 = \frac{2}{3} - \left(\frac{1}{2}\right)^2 = \frac{5}{12} $

したがって，

$\displaystyle D(X) = \sqrt{V(X)} = \sqrt{\frac{5}{12}} $

c Standardization of 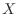$X$ means changing the mean $\mu$ to 0 and the distribution $\sigma^2$ to 1. Then

$\displaystyle Z = \frac{X - \mu}{\sqrt{\sigma^2}} = \frac{X - \frac{1}{2}}{\sqrt{\frac{1}{6}}} $

Find the probabilty distribution of $Z$．

$\displaystyle P_{r}(X = 0) = P_{r}\left(\frac{X - \frac{1}{2}}{\sqrt{\frac{5}{1... ...0 - \frac{1}{2}}{\sqrt{\frac{5}{12}}}\right) = P_{r}(Z = - \sqrt{\frac{3}{5}}) $

Then

$\displaystyle P_{r}(Z = - \sqrt{\frac{3}{5}}) = P_{r}(X = 0) = \frac{125}{216} $

$\displaystyle P_{r}(X = 1) = P_{r}\left(\frac{X - \frac{1}{2}}{\sqrt{\frac{5}{1... ...c{1 - \frac{1}{2}}{\sqrt{\frac{5}{12}}}\right) = P_{r}(Z = \sqrt{\frac{3}{5}}) $

Then

$\displaystyle P_{r}(Z = \sqrt{\frac{3}{5}}) = P_{r}(X = 0) = \frac{25}{72} $

$\displaystyle P_{r}(X = 2) = P_{r}\left(\frac{X - \frac{1}{2}}{\sqrt{\frac{5}{1... ...{2 - \frac{1}{2}}{\sqrt{\frac{5}{12}}}\right) = P_{r}(Z = \frac{3\sqrt{3}}{5}) $

Then

$\displaystyle P_{r}(Z = \frac{3\sqrt{3}}{5}) = P_{r}(X = 0) = \sqrt{\frac{25}{72}} $

$\displaystyle P_{r}(X = 3) = P_{r}\left(\frac{X - \frac{1}{2}}{\sqrt{\frac{5}{1... ...{3 - \frac{1}{2}}{\sqrt{\frac{5}{12}}}\right) = P_{r}(Z = \frac{5\sqrt{3}}{5}) $

Then

$\displaystyle P_{r}(Z = \frac{5\sqrt{3}}{5}) = P_{r}(X = 0) = \sqrt{\frac{1}{216}} $

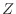3

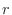a Bernoulli's theorem is when the number of trials is $n$, the number of event occurrences is $r$, and the probability of event occurrence is $p$. Then

$\displaystyle P_{r}(\vert\frac{r}{n} - p\vert \leq \varepsilon) \geq 1 - \frac{p(1-p)}{n \varepsilon^2} $

$\displaystyle P_{r}(\vert\frac{r}{1000} - \frac{1}{2}\vert \leq \frac{1}{10}) \geq 1 - \frac{\frac{1}{2}(1-\frac{1}{2})}{1000 (\frac{1}{10})^2} = \frac{39}{40}$

b

$\displaystyle P_{r}(\vert\frac{r}{1000} - \frac{1}{4}\vert \leq \frac{1}{10}) \geq 1 - \frac{\frac{1}{4}(1-\frac{1}{4})}{1000 (\frac{1}{10})^2} = \frac{3}{160}$

c The problem is to find the probability that the bias of the number of event occurrences 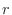$r$ is within 50 when the number of trials is 2000. In other words, find the probability that the error between the percentage of heads appearing in 2000 times $\frac{r}{2000}$ and the theoretical probability $p = \frac{1}{2}$ is $\frac{50}{1000}$. Then using Bernoulli's theorem,

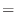$\displaystyle P(\vert\frac{r}{n} - p\vert \leq \varepsilon) \geq 1 - \frac{p(1-p)}{n \varepsilon^2} $

Thus,
$\displaystyle P(\vert\frac{r}{2000} - \frac{1}{2}\vert < \frac{50}{1000})$ $\displaystyle \geq$ $\displaystyle 1 - \frac{\frac{1}{2}(1-\frac{1}{2})}{2000 (\frac{1}{20})^2}$  
  $\displaystyle =$ $\displaystyle 1 - \frac{\frac{1}{4}}{5} = 1 - 0.05 = 0.95$  

d

$\displaystyle P(\vert\frac{r}{n} - p\vert \leq \varepsilon) \geq 1 - \frac{p(1-p)}{n \varepsilon^2} $

implies that we find $n$ so that $1 - \frac{p(1-p)}{n \varepsilon^2} \geq 0.99$．
$\displaystyle 1 - \frac{\frac{1}{2}(1-\frac{1}{2})}{n (0.05)^2} \geq 0.99 \Rightarrow$      
$\displaystyle \frac{\frac{1}{2}(1-\frac{1}{2})}{n (0.05)^2} \leq 0.01 \Rightarrow$      
$\displaystyle n \geq \frac{1}{4(0.05)^2 0.01} = 10000$      

next up previous contents
Next: Multidimensional probability distribution Up: Random variables Previous: Two-dimensional probability distribution   Contents