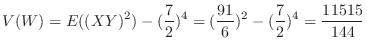Next: Theoretical distribution Up: Random variables Previous: Mean and variance of Contents
1. If one bronze coin is thrown and the front side appears, it is expressed as 1, and if the back side appears, it is expressed as 0. Answer the following questions, setting the random variables for the appearance of each bronze coin table as 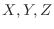 when throwing three bronze coins.
when throwing three bronze coins.
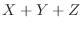 .
.
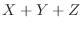 .
.
2. The probability density of 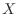 is given by the
is given by the
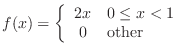
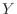 and
and 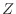 .
.
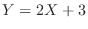
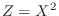
3. Let the random variables 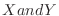 be the rolls of the two dice
be the rolls of the two dice
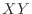 .
.
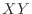 .
.
1.
a Let
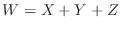 . Then the domain of
. Then the domain of 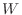 is
is
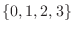 .The probabilty istribution
.The probabilty istribution 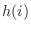 is given by
is given by 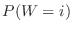 .
Consider
.
Consider 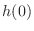 .
.
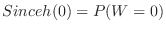 ,It's the same as throwing three bronze coins and finding the probability that all tails come out. All tail combinations are 1 out of 8.Thus,
,It's the same as throwing three bronze coins and finding the probability that all tails come out. All tail combinations are 1 out of 8.Thus,
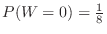 .Similarly for
.Similarly for 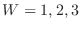 ,
,
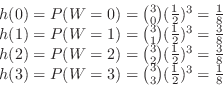
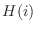 . Since
. Since
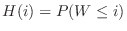 ,
,
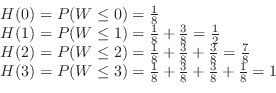
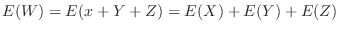
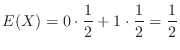
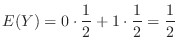
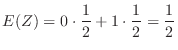
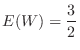
2.
a To find the probability density function 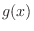 of
of 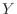 , examine the distribution function
, examine the distribution function 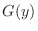 of
of 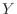 and use the relation of
and use the relation of
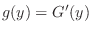 .
.
The distribution function 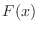 of
of 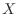 is
is
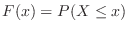 , and the distribution function
, and the distribution function 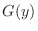 of
of 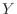 is
is
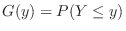 given by
given by
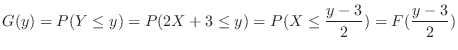
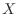 is given by
is given by
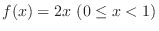 , so the probability density function
, so the probability density function 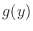 of
of 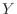 is,
is,
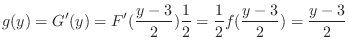
The expectation of 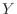 is
is
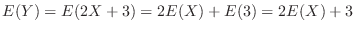 . Then to find
. Then to find 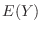 , it is enough to find
, it is enough to find 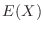 .
.
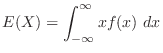 . Then
. Then
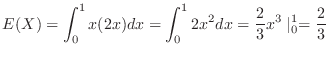
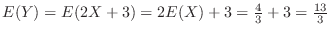
Note : Since the probability density function of 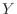 was calculated, directly calculate
was calculated, directly calculate 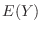 by
by
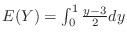 .
.
Finally, we find the variance of 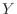 .Note that
.Note that
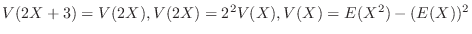 . Then to find
. Then to find 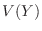 , we need to find
, we need to find 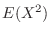 .
.
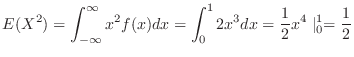
![$\displaystyle V(Y) = V(2X+3) = 4V(X) = 4[E(X^2) - (E(X))^2] = 4[\frac{1}{2} - (\frac{2}{3})^2] = \frac{2}{9}$](img336.png)
b
To find the probability density function 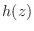 of
of 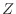 , examine the distribution function
, examine the distribution function 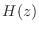 of
of 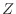 and use the relation of
and use the relation of
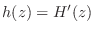
The distribution function 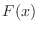 of
of 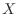 is
is
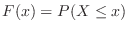 , and the distribution function
, and the distribution function 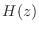 of
of 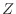 is
is
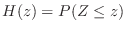 . Since it is given by,
. Since it is given by,
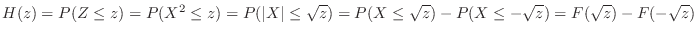
Thus the probability density function 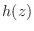 of
of 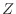 is
is
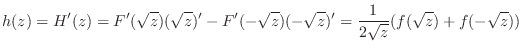
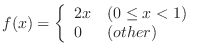
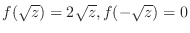 .Therefore,,
.Therefore,,
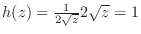 .
.
We next find the expectation..
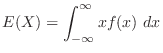 .
.
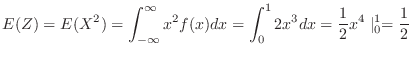
Finally, find the variance of 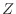 .
.
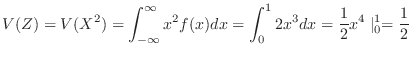
![$\displaystyle V(Y) = V(2X+3) = 4V(X) = 4[E(X^2) - (E(X))^2] = 4[\frac{1}{2} - (\frac{2}{3})^2] = \frac{2}{9}$](img336.png)
3.
a Let 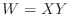 . Then
. Then 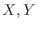 are independent and the expectation is given by
are independent and the expectation is given by
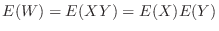
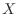 is the value of the pip that appears when one die is thrown, its expected value
is the value of the pip that appears when one die is thrown, its expected value 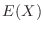 is
is
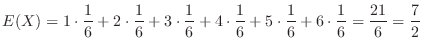
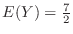 . Then the expectation
. Then the expectation 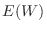 is
is
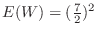 .
.
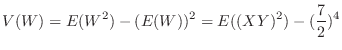
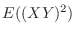 .Note that
.Note that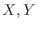 are independent. Then
are independent. Then
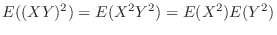
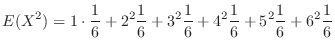
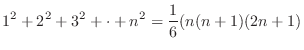
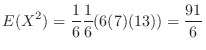
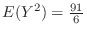 and
and 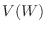 is
is