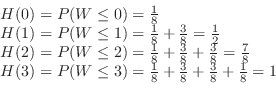Next: Mean and variance of Up: Random variables Previous: Random variables Contents
1.
Find the probability distribution and distribution function of the product 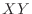 , where
, where 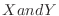 are the random variables for the two dice pips.
.
are the random variables for the two dice pips.
.
2. If one bronze coin is thrown and the face comes out, it is expressed as 1, and if the tail comes out, it is expressed as 0. When throwing three bronze coins, let 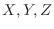 be the random variables for the appearance of each bronze coin.
be the random variables for the appearance of each bronze coin.
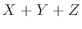 .
.
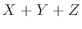 .
.
(1) Let 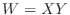 . Then the domain of
. Then the domain of 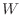 is
is
 .Also note that the probability distribution
.Also note that the probability distribution 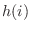 is given by
is given by 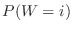 .
First consider
.
First consider  .Since
.Since
 ,
It's the same as throwing two dice and finding the probability of both rolling one. The combination of both 1's pips is 1 out of 36 ways.Thus
,
It's the same as throwing two dice and finding the probability of both rolling one. The combination of both 1's pips is 1 out of 36 ways.Thus
 .Similarly,we fin for
.Similarly,we fin for
 ,
,

(2)
a Let
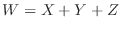 . Then the domain of
. Then the domain of 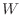 is
is
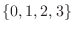 and the probabilty distribution
and the probabilty distribution 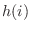 is given by
is given by 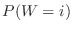 .
.
First consider 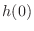 .Since
.Since
 ,
It's the same as throwing three bronze coins and finding the probability that all of them will come out. All tails combinations are 1 out of 8.Thus
,
It's the same as throwing three bronze coins and finding the probability that all of them will come out. All tails combinations are 1 out of 8.Thus
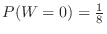 .Similarly we find for
.Similarly we find for 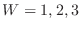 ,
,
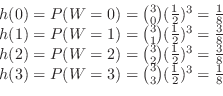
b Find the distribution function 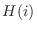 . Since
. Since
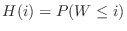 ,we have
,we have