Complex integration

Let $\Omega$ be the region containing the curve $C$

on the

plane, and let $f(z)$

be a continuous function defined on $\Omega$ so that

$\displaystyle f(z) = u(x,y) + i v(x,y)$

Then

$\displaystyle f(z)\frac{dz}{dt}$	$\displaystyle =$	$\displaystyle (u(x,y) + i v(x,y))(\frac{dx}{dt} + i \frac{dy}{dt})$
	$\displaystyle =$	$\displaystyle u\frac{dx}{dt} - v \frac{dy}{dt} + i (v\frac{dx}{dt} + u \frac{dy}{dt})$

Here, The first term of the last equation is a function of the parameter $t$

, the integral

$\displaystyle \int_{\alpha}^{\beta}u(x(t),y(t))\frac{dx}{dt}\; dt = \int_{C}u\; dx$

does not depend on $t$

and it is a line integral of $u$

along the curve $C$

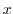. Thinking about the remaining terms in the same way, the next integral can be considered.

$\displaystyle \int_{C}u\;dx - \int_{C}v\;dy + i(\int_{C}v\; dx + \int_{C}u \;dy)$

This is called bf integral along the curve $C$

of the function $f(z)$

and expressed by

$\displaystyle \int_{C}f(z)\;dz$

This is given in the range of complex numbers. We say complex integral.

Exercise4.2

1 Find $\int_{C}z\cos{z}dz$ along the curve $C$

that goes around the unit circle.

2 Integrate the function $\bar{z}$ for along the sides and diagonals of a square with vertices at point $0,1,1 + i, i$ from 0 to $1+i$ .