Line integral and Green's theorem

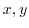$P(x,y)$ and $Q(x,y)$ are real-valued functions of $x,y$ and continuous on every point on the curve $C$ . Then the line integral of $P\;dx + Q\;dy$ along the curve $C$ is defined by

$\displaystyle \int_{C} [P(x,y)\;dx + Q(x,y)\;dy]$

Now if the curve $C$

is smooth and it is possible to parametrize by $x = \phi(t), y = \psi(t)$ , $t_{1} \leq t \leq t_{2}$ , then the line integral is given by

$\displaystyle \int_{t_{1}}^{t_{2}}[P(\phi(t),\psi(t))\;dt + Q(\phi(t),\psi(t))\;dt]$

Theorem 4..1 (Green's theorem)

Let be a single closed curve and $\Omega$ be a closed region consisting of its boundary and its interior. If functions have continuouspartial derivatives on $\Omega$ , then

$\displaystyle \int_{C}Pdx + Qdy = \iint_{\Omega}(\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y})\;dx\;dy$

Exercise4.1

1. Find the following line integrals.

(a): $\int_{c}y dx, C: y = 1 -x, 0 \leq x \leq 1$
(b): $\int_{c}x^2 dy, C: y = 1 -x, 0 \leq x \leq 1$
(c): $\int_{c}(xy dx - y^2 dy), C: y = x^2, -1 \leq x \leq 1$
(d): $\int_{c}(xy dx - x^3 dy), C: x = \cos{\theta}, y = \sin{\theta}, 0 \leq \theta \leq 2\pi$

2. Find the following line integral for the parameter $t$

(a): $\int_{c}(x^2 + y)dt, C: x = \sqrt{t}, y = 1 - t^2, 0 \leq t \leq 1$
(b): $\int_{c}xy^2 dt, C: x = \sin{t}, y = \sin^{2}{t}, 0 \leq t \leq \frac{\pi}{2}$

3. Using Green's theorem, evaluate the following line integral.

(a): $\int_{c}(x^2 y dx - xy^2 dy), C:$ unit circle
(b): $\int_{c}(y dx + 2x dy), C:$ first quadrand quater circle