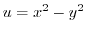Next: Cauchy's integral formula Up: Complex integration Previous: Complex integration Index
 is analytic in the region
is analytic in the region  , let
, let  be any single closed curve in
be any single closed curve in  , and the region
, and the region
 surrounded by
surrounded by  is inside
is inside  . Then
. Then

 is analytic in the region
is analytic in the region  , and the two curves
, and the two curves
 connecting the two points
connecting the two points  and
and  are in
are in  and if the area enclosed by
and if the area enclosed by
 is in
is in  , then
, then

 is analytic in the region
is analytic in the region  surrounded by two single closed curves
surrounded by two single closed curves
 , then
, then

2. Integrate the following function along the shown closed curve.
 centered at the origin and a circle with the radius
centered at the origin and a circle with the radius  .
.
 unit circle
unit circle
 centered at the origin and a semicircle with the radius
centered at the origin and a semicircle with the radius  and the diameter on the real axis.
and the diameter on the real axis.
3. Find the following integral. The integration path is a line segment connecting the lower end and the upper end.




4. Prove the following functions are harmonic functions and Create a holomorphic function that has it in the real part.