Matrix Factorization

Gaussian elimination is the most important tool for solving a linear system. In this section, we will see that the the steps used to solve a system of the form $A{\bf x} = {\bf b}$ can be used to factor a matrix. The factorization is particularly useful when it has the form $A = LU$, where $L$ is lower triangular and $U$ is upper triangular.

Now how do we factor $A = LU$?

$$\begin{array}{rrrrrr} x_{1}& + x_{2}& & + 3x_{4}& =& 4\\ 2x_... ... =& -3\\ -x_{1}& + 2x_{2}& + 3x_{3}& - x_{4}& =& 4 \end{array}$$

Then the coefficient marix is given by

$${A}^{(1)} = \left(\begin{array}{rrrr} 1 & 1 & 0 & 3\\ 2 & 1 & -1 & 1\\ 3 & -1 & -1 & 2\\ -1 & 2 & 3 & -1 \end{array}\right)$$

Since $a_{11}^{(1)} = 1 \neq 0$, the multiples are $m_{2,1} = 2, m_{3,1} = 3, m_{4,1} = -1$. Now by the elementary row operations $-2R_{1} + R_{2} \to R_{2}$, $-3R_{1}+R_{3} \to R{3}$, $R_{1} + R_{4} \to R_{4}$, we have

$${A}^{(2)} = \left(\begin{array}{rrrr} 1 & 1 & 0 & 3\\ 0 & -1 & -1 & -5\\ 0 & -4 & -1 & -7\\ 0 & 3 & 3 & 2 \end{array}\right)$$

Next since the pivot $a_{22}^{(2)} = -1 \neq 0$，the multiples are $m_{3,2} = 4, m_{4,2} = -3$. Now by the elementary row operations $-4R_{2} + R_{3} \to R_{3}$, $3R_{2}+R_{4} \to R_{4}$, we have

$${A}^{(3)} = \left(\begin{array}{rrrr} 1 & 1 & 0 & 3\\ 0 & -1 & -1 & -5\\ 0 & 0 & 3 & 13\\ 0 & 0 & 0 & -13 \end{array}\right)$$

$A^{(3)}$ is an upper triangular. So, set $A^{(3)} = U$. Then we have $U$. Now how do we find $L$. We recall elementary row operations we used to find $U$. Thenapplying $-2R_{1} + R_{2} \to R_{2}$, $-3R_{1}+R_{3} \to R_{3}$, $R_{1} + R_{4} \to R_{4}$ is the same as multiplying

$$M^{(1)} = \left(\begin{array}{rrrr} 1 & 0 & 0 & 0\\ -m_{2,1} & 1 & 0 & 0\\ -m_{3,1} & 0 & 1 & 0\\ -m_{4,1} & 0 & 0 & 1 \end{array}\right)$$

to ${A}^{(1)}$. This matrix is called first Gaussian transformation matrix. Next elementary row operations $-4R_{2} + R_{3} \to R_{3}$, $3R_{2}+R_{4} \to R_{4}$ are applied to $A^{(2)}$ and the second Gaussian transformation matrix $M^{(2)}$ is

$$M^{(2)} = \left(\begin{array}{rrrr} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & -m_{3,2} & 1 & 0\\ 0 & -m_{4,2} & 0 & 1 \end{array}\right)$$

In other words,

$$U = A^{(3)} = M^{(2)}A^{(2)} = M^{(2)}M^{(1)}A^{(1)} = M^{(2)}M^{(1)}A$$

Then $L = (M^{(1)})^{-1} (M^{(2)})^{-1}$. Note that if we set $(M^{(1)})^{-1} = L^{(1)},(M^{(2)})^{-1} = L^{(2)}$，then $L = L^{(1)}L^{(2)}$. Since $\det M^{(1)} = \det M^{(2)} = 1$，we have

$$L^{(1)} = (M^{(1)})^{-1} = \left(\begin{array}{rrrr} 1 & 0 & 0 & ... ...1} & 1 & 0 & 0\\ m_{3,1} & 0 & 1 & 0\\ m_{4,1} & 0 & 0 & 1 \end{array}\right)$$

$$L^{(2)} = (M^{(2)})^{-1} = \left(\begin{array}{rrrr} 1 & 0 & 0 & ... ... 0 & 1 & 0 & 0\\ 0 & m_{3,2} & 1 & 0\\ 0 & m_{4,2} & 0 & 1 \end{array}\right)$$

Thus,

$$L = L^{(1)}L^{(2)} = \left(\begin{array}{rrrr} 1 & 0 & 0 & 0\\ m... ... 0 & 0\\ 2 & 1 & 0 & 0\\ 3 & 4 & 1 & 0\\ -1 & -3 & 0 & 1 \end{array}\right).$$

We note that the diagonal elements of the matrix $L$ are all $1$.

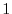Generalizing this, we have the following.

Theorem 2..12   If Gaussian elimination can be performed on the the matrix $A$ without row interchanges, then the matrix $A$ can be factored into the prouct of a lower-triangular matrix $L$ and an upper-triangular matrix $U$ so that $A = LU$, where $m_{ji} = a_{ji}^{(i)}/a_{ii}^{(i)}$,

$$U = \left(\begin{array}{cccccc} a_{11}^{(1)} & a_{12}^{(1)} & \cd... ...n}^{(n-1)}\\ 0 & \cdots & \cdot & \cdots & 0 & a_{nn}^{(n)} \end{array}\right)$$

$$L = \left(\begin{array}{cccccc} 1 & 0 & \cdots & \cdots & \cdots ... ... & & \ddots & 0\\ m_{n,1} & \cdots & \cdot & \cdots & 0 & 1 \end{array}\right)$$

Exercise2-7

1. Solve the following linear system

$\left(\begin{array}{rrr} 1 &0&0\\ 2&1&0\\ -1&0&1 \end{array}\right)\left(... ...\end{array}\right) = \left(\begin{array}{r} 2\\ -1\\ 1 \end{array}\right)$

2. Factor the following matrices into the $LU$ decomposition.

(a) $\left(\begin{array}{rrr} 2&-1&1\\ 3&3&9\\ 3&3&5 \end{array}\right)$

(b) $\left(\begin{array}{rrrr} 2&0&0&0\\ 1&1.5&0&0\\ 0&-3&0.5&0\\ 2&-2&1&1 \end{array}\right)$