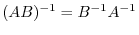Next: Matrix Factorization Up: Matrix and Determinant Previous: Elementary Row Operation Contents Index
We have introduced Guassian elimination in 2.2. Here we study whether the given system of linear equation has a solution. To start with, we consider the system of linear equation with the unkowns and the number of equations are different.
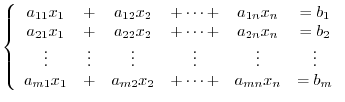
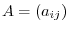 be a matrix,
be a matrix,
![$[A : {\bf b}]$](img676.png) be the augmented matrix,
be the augmented matrix,  be the number of unknowns,
be the number of unknowns,
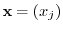 be the row vectors, and
be the row vectors, and
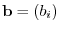 be the column vetors of the order
be the column vetors of the order 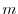 . Then the system of linear equations is written as
. Then the system of linear equations is written as
![$\displaystyle A{\mathbf x} = {\bf b} \mbox{または} [A : {\bf b}] $](img679.png)
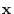 and this vector is called solution vector. In general, the following holds.
and this vector is called solution vector. In general, the following holds.
![$\displaystyle {\rm rank}(A) \leq {\rm rank}([A : {\bf b}]) \leq {\rm rank}(A) + 1 $](img680.png)
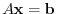 has a solution if and only if
has a solution if and only if
![$\displaystyle {\rm rank}(A) = {\rm rank}([A : {\bf b}]) $](img682.png)
Proof
Let  be a matrix of the form
be a matrix of the form
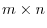 . Suppose that
. Suppose that
![${\rm rank}(A) = {\rm rank}([A : {\bf b}]) = r$](img683.png) . Then the dimension of the column space of
. Then the dimension of the column space of
![$[A : {\bf b}]$](img676.png) is
is 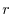 and
and 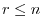 . Thus,
. Thus, 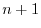 st column vectorb of the column space
st column vectorb of the column space
![$[A : {\bf b}]$](img676.png) is a linear combination of
is a linear combination of
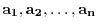
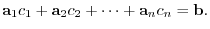
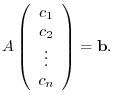
Conversely, think of columns of  as column vectors. Thne the equation
as column vectors. Thne the equation
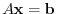 can be expressed as
can be expressed as
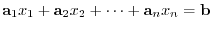
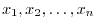 , then this equation implies that
, then this equation implies that 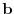 is a linear combination of
is a linear combination of
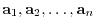
 and the column space of
and the column space of
![$[A : {\bf b}]$](img676.png) are the same. This shows that
are the same. This shows that
![${\rm rank}(A) = {\rm rank}([A : {\bf b}])$](img693.png) .
.

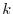 so that the following equation has a solution.
so that the following equation has a solution.
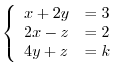
Answer
![$\displaystyle [A: {\bf b}]$](img695.png) |
 |
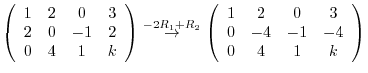 |
|
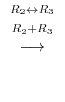 |
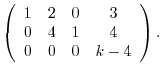 |
![${\rm rank}([A: {\bf b}]) = {\rm rank}A = 2$](img699.png) . Thus
. Thus 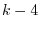 must be 0. Therefore
must be 0. Therefore 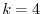 .
.

 General solution of system of linear equation
General solution of system of linear equation

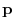 be a pair of solution to the system of linear equations
be a pair of solution to the system of linear equations
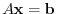 . Then every solution of
. Then every solution of
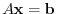 is given by
is given by
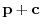 . Here,
. Here, 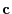 is a solution of
is a solution of
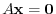 .
.
Proof
Let 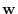 be a solution of
be a solution of
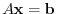 . Then,
. Then,
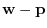 is a solution of
is a solution of
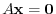 since
since
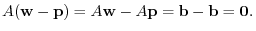
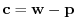 . Then
. Then 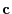 is a solution of
is a solution of
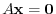 . Thus, we have
. Thus, we have
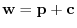 .
.

With this theorem, to solve the system of linear equations
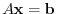 , we first need to solve the homogeneous system
, we first need to solve the homogeneous system
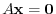 . So, we consider the homogeneous system of linear equations
. So, we consider the homogeneous system of linear equations
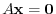 .
.
Note that
![${\rm rank}(A) = {\rm rank}([A : {\bf0}])$](img711.png) . Then by the theorem 2.3, a solution exists. In fact,
. Then by the theorem 2.3, a solution exists. In fact,
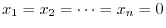 is a solution. This solution is called trivial solution. Next Let
is a solution. This solution is called trivial solution. Next Let  numbers of nontrivial solutions of the system of linear equations be the followings:
numbers of nontrivial solutions of the system of linear equations be the followings:
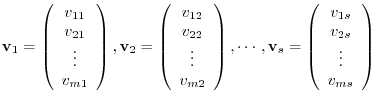
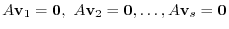
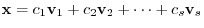 satisfies
satisfies
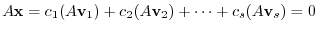 Thus,
Thus,
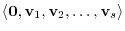 is a subspace. This subspace is called solution space. The basis of this solution space is called an (elementary solution of the system of linear equation
is a subspace. This subspace is called solution space. The basis of this solution space is called an (elementary solution of the system of linear equation
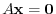 .
.
It is interesting to know the relationship between the dimension of the solution space and the rank of the matrix.
 unknowns
unknowns
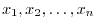 . Suppose the rank of the coefficient matrix
. Suppose the rank of the coefficient matrix  is
is 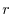 , then the fundamental solution is composed of the
, then the fundamental solution is composed of the 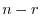 solution vectors.
solution vectors.
Proof
For
![${\rm rank}(A) = {\rm rank}([A : {\bf0}]) = r$](img720.png) , apply the elementry row operation on
, apply the elementry row operation on
![$[A : {\bf0}]$](img721.png) to obtain the followings:
to obtain the followings:
![$\displaystyle [A : {\bf0}]_{R} = \left(\begin{array}{rrrrrrcr}
1&\cdots&0&d_{1 ...
...ts& &\vdots&\vdots&\vdots\\
0&\cdots&0&0&\cdots&0&\vdots&0
\end{array}\right) $](img722.png)
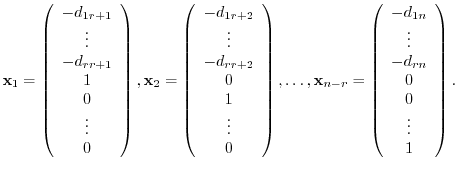
 are solution vectors. Also, let
are solution vectors. Also, let
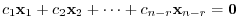
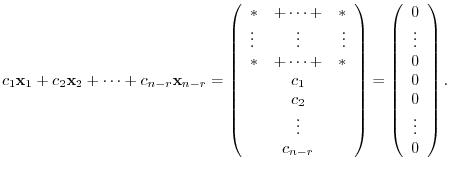
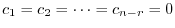 . Thus,
. Thus,
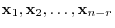 is linearly independent. Therefore the dimension of the solution space is
is linearly independent. Therefore the dimension of the solution space is 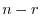 .
.

 Degree of freedom
Degree of freedom

The number of elementary solutions 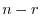 is called a degree of freedom.
is called a degree of freedom.
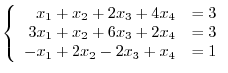
Answer
Apply Gaussian elimination..
![$\displaystyle [A: {\bf b}]$](img695.png) |
 |
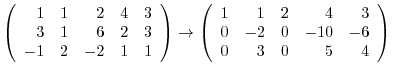 |
|
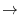 |
![$\displaystyle \left(\begin{array}{rrrrr}
1&0&2&-1&0\\
0&1&0&5&3\\
0&0&0&1&\fr...
...&0&0&\frac{1}{2}\\
0&0&0&1&\frac{1}{2}
\end{array}\right) = [A: {\bf b}]_{R} .$](img731.png) |
![${\rm rank}(A) = {\rm rank}([A : {\bf b}]) = 3$](img732.png) which implies that this system of linear equation has a solution. If we write
which implies that this system of linear equation has a solution. If we write
![$[A:{\bf b}]_{R}$](img733.png) as a system of linear equatios:
as a system of linear equatios:
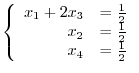
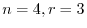 . Thus the defree of freedom is
. Thus the defree of freedom is 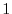 . Then we let
. Then we let
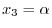 and we have the followings:
and we have the followings:
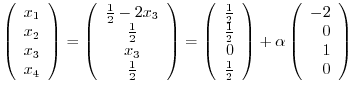

 Inverse Matrix
Inverse Matrix

Consider the matrix
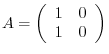 .
.  is not zeor matrix. Now we ask you a question. Do we have a matrix
is not zeor matrix. Now we ask you a question. Do we have a matrix 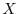 so that
so that
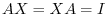 . Unfortunately, the answer is no. In the world of matrices, some nonzero matrix does not have inverse.
. Unfortunately, the answer is no. In the world of matrices, some nonzero matrix does not have inverse.
 Regular Matrix
Regular Matrix

For the square matrix  of the order
of the order , if there exists a matrix
, if there exists a matrix 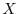 so that
so that
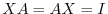 , then the matrix
, then the matrix  is called a regular matrix. The matrix
is called a regular matrix. The matrix 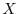 is called an inverse matrix of
is called an inverse matrix of  . Now how many inverse matrices of
. Now how many inverse matrices of  exist? For example,
exist? For example,
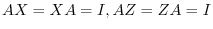 . Then
. Then
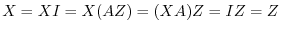 . Thus, the inverse matrix of
. Thus, the inverse matrix of  is one. Then we write the inverse matrix of
is one. Then we write the inverse matrix of  as
as 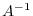 .
.
Using this idea, we solve the system of linear equations
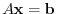 . Let
. Let  be a regular matrix. Then we have
be a regular matrix. Then we have
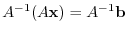 . From this, we have
. From this, we have
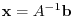 . Therefore, to solve the system of linear equations, we can use the inverse matrix
. Therefore, to solve the system of linear equations, we can use the inverse matrix 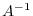 . In short, it is enough to find a matrix
. In short, it is enough to find a matrix 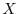 so that
so that 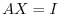 We know a quick way to find
We know a quick way to find 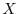 . Before introducing the technique, we cover the relation between the regular matrix and the rank of the matrix.
. Before introducing the technique, we cover the relation between the regular matrix and the rank of the matrix.
 is a squre matrix with the order of
is a squre matrix with the order of  . Then the followings are equivalent.
. Then the followings are equivalent.
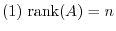
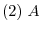 is regular matrix.
is regular matrix.
Proof
By theorem 2.2,
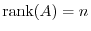 and
and 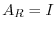 are equivalent.
In other words, for
are equivalent.
In other words, for
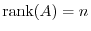 , we can choose the product of elementary matrices
, we can choose the product of elementary matrices  so that
so that 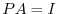 . Thus,
. Thus,  is regular.
is regular.
Conversely, for  is a regular matrix, we can choose a product of elementary matrices
is a regular matrix, we can choose a product of elementary matrices  so that
so that
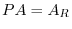 . Note that
. Note that  is the product of elementary matrices. Then
is the product of elementary matrices. Then  is regular. Thus,
is regular. Thus, 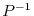 exists. Suppose that
exists. Suppose that
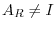 . Then the entries of the lowest row of
. Then the entries of the lowest row of 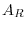 have to be 0. But then this matrix is not regular. Thus,
have to be 0. But then this matrix is not regular. Thus,
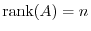 .
.

Now we are ready to introduce how to find a matrix 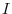 satisfying
satisfying 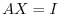 . We note that since
. We note that since  is regular, for some product
is regular, for some product  of elementary matrices,
of elementary matrices, 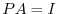 . So, we multiply this
. So, we multiply this  to
to 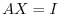 from the left. Then
from the left. Then
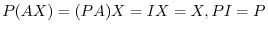 . Thus to find
. Thus to find 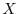 is the same as to find
is the same as to find  . This shows that if you can get the identiry matrix by applying elementary row operation to
. This shows that if you can get the identiry matrix by applying elementary row operation to  , the the same operation on
, the the same operation on 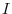 gives rise to
gives rise to 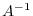 .
.
 is regular. If so, find the inverse matrix of
is regular. If so, find the inverse matrix of  where
where
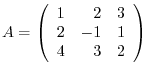 .
.
Answer
![$\displaystyle [A:I]$](img755.png) |
 |
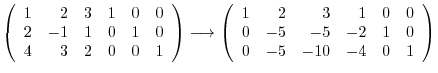 |
|
 |
 |
||
 |
![$\displaystyle \left(\begin{array}{rrrrrr}
1&0&0&-\frac{1}{5}&\frac{1}{5}&\frac{...
...
0&0&1&\frac{2}{5}&\frac{1}{5}&-\frac{1}{5}
\end{array}\right ) = [I:A^{-1}] .$](img759.png) |
 is regular and
is regular and
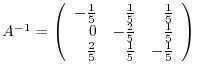 .
.

Summarize what we have studied so far, we have
 is the square matrix of the order
is the square matrix of the order  . Then the followings are equivalent.
. Then the followings are equivalent.
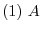 is regular
is regular
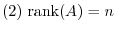
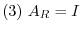
Proof
By theorem 2.2, we have
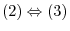 . By theorem 2.3, we have
. By theorem 2.3, we have
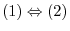 .
.
1. Solve the following system of linear equations using Gaussian elimination.
2. Determine the value of 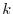 so that the following system of linear equations has a solution.
so that the following system of linear equations has a solution.
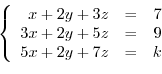
3. Determine whether the following matrix is regular. If so, find the inverse matrix,
(a)
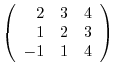
4. Determine the value 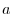 so that the following matrix is regular.
so that the following matrix is regular.

5. Show that the following matrix is regular, and show the following matrix as a product of elementary matrices.
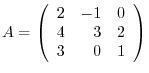 .
.
6. Suppose that all entries of one row of the square matrix are 0. The show that  is not regular.
is not regular.
7. Suppose that 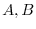 are regular matrices of the order
are regular matrices of the order  . Then show thatthe product of
. Then show thatthe product of 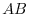 is also regular and satisfies
is also regular and satisfies