Next: 演習問題 Up: フーリエ級数 Previous: 演習問題 目次 索引
![$PC[a,b]$](img1696.png) は内積
は内積
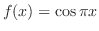
![$\displaystyle \vert\vert f\vert\vert = (\int_{a}^{b}[f(x)]^{2}dx)^{1/2} $](img1742.png)
ここでは周期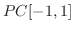 をもつ周期関数
をもつ周期関数
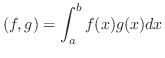
![$PC[-L,L]$](img1745.png) 上で考えます.
上で考えます.
前節で学んだように次の関数列は![$[-L,L]$](img1746.png) 上で直交系をなします.
上で直交系をなします.
1.
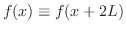
2.
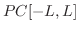
3.
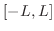
4. 3で与えられた集合の部分集合
ここで幾何ベクトル
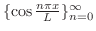 のときのようにこの直交系を用いてベクトル空間
のときのようにこの直交系を用いてベクトル空間![$PC[-L,L]$](img1745.png) 内のベクトルを一次結合で表わすことができないでしょうか.つまり
内のベクトルを一次結合で表わすことができないでしょうか.つまり
![$f(x) \in PC[-L,L]$](img1751.png) のとき
のとき
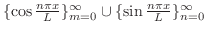
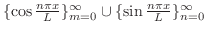
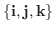 |
 |
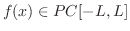 |
|
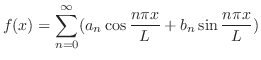 |
 |
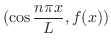 |
|
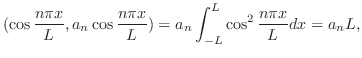 |
 |
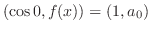 |
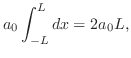 |
 |
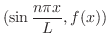 |
|
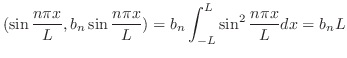 |
 |
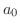 |
|
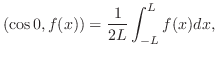 |
 |
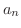 |
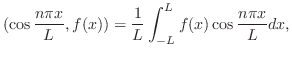 が決定されます.
が決定されます.
しかし,三角級数
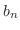 は収束すると限らないし,収束したとしても,もとの関数
は収束すると限らないし,収束したとしても,もとの関数 に一致するとは限りません(4章参照).そこで,関数
に一致するとは限りません(4章参照).そこで,関数 とこのようにして定められた三角級数との関係を,等号
とこのようにして定められた三角級数との関係を,等号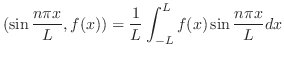 の変わりに
の変わりに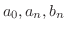 を用いて表わすことにします.以上をまとめると
を用いて表わすことにします.以上をまとめると
|
定義 6..5 (フーリエ級数)
![$f(x) \equiv f(x+2L), f(x) \in PC[-L,L]$](img1769.png) のとき, のとき,
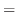
|
このとき
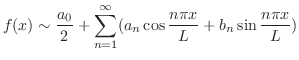 を
を のフーリエ(三角)級数とよび,
のフーリエ(三角)級数とよび,
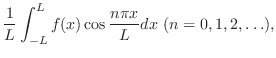 を
を の第n部分和とよびます.
の第n部分和とよびます.
![$f(x) = x \in PC[-\pi,\pi]$](img1775.png) のとき,
のとき, のフーリエ級数を求めよ.また第n部分和のグラフを調べよ.
のフーリエ級数を求めよ.また第n部分和のグラフを調べよ.
解
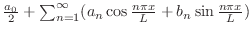 は奇関数であることに注意すると
は奇関数であることに注意すると
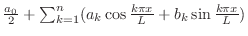
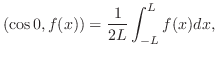 |
 |
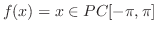 |
|
 |
![$\displaystyle \frac{2}{\pi}[-\frac{x\cos{nx}}{n}\mid_{0}^{\pi} + \frac{1}{n}\int_{0}^{\pi}\cos{nx}dx]$](img1779.png) |
||
 |
![$\displaystyle \frac{2}{\pi}[-\frac{\pi\cos{n \pi}}{n} + \frac{1}{n^2}\sin{nx}\mid_{0}^{\pi}]$](img1780.png) |
||
 |
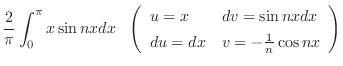 |
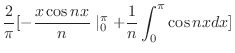
解
 |
 |
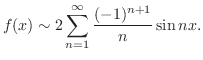 |
|
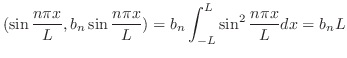 |
 |
 |
|
 |
 |
 |
|
 |
![$\displaystyle \frac{1}{\pi}[\frac{-2\cos{nx}}{n}\mid_{-\pi}^{0} - \frac{\cos{nx}}{n}\mid_{0}^{\pi}]$](img1788.png) |
||
 |
![$\displaystyle \frac{1}{n\pi}[-2 + 2\cos{n\pi} - \cos{n\pi} + 1 ]$](img1789.png) |
||
 |
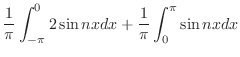 |
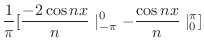
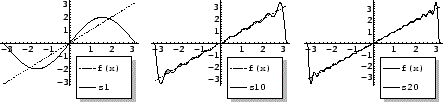
部分和のグラフをみると,関数 が不連続の点の近くで,部分和のグラフが
が不連続の点の近くで,部分和のグラフが のグラフよりかなり大きな値をとっていることがわかります.これをovershootといいます.また部分和のグラフは不連続点の近くで垂直な線分に近づいていることがわかります.これをGibbs 現象といいます.
のグラフよりかなり大きな値をとっていることがわかります.これをovershootといいます.また部分和のグラフは不連続点の近くで垂直な線分に近づいていることがわかります.これをGibbs 現象といいます.
次にフーリエ級数が に収束するための条件を紹介します.
に収束するための条件を紹介します.
![$f(x) \in PC[-L,L], f^{\prime}(x) \in PC[-L,L]$](img1793.png) ならば
ならば
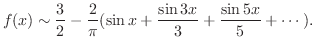
![$f(x), f^{\prime}(x) \in PC[-L.L]$](img1795.png) であるような関数を区分的に滑らか(piecewise smooth)な関数といいます.
であるような関数を区分的に滑らか(piecewise smooth)な関数といいます.
解 例題6.6より
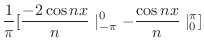
 はDirichlet条件を満たすので
はDirichlet条件を満たすので
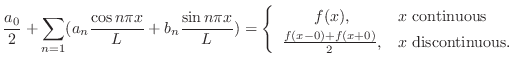
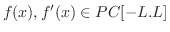
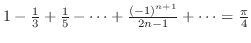
ベクトル
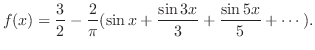 のノルム
のノルム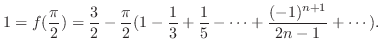 が
が
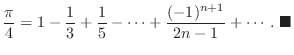
![$f(x) \in PC[-L,L]$](img1751.png) は次の等式を満たします.
は次の等式を満たします.
![$\displaystyle \vert\vert f\vert\vert^{2} = L[\frac{a_{0}^{2}}{2} + \sum_{n=1}^{\infty}(a_{n}^{2} + b_{n}^{2})] . $](img1803.png)
この等式をParseval の等式といいます.