Next: 2.3 解答 Up: 演習問題解答 Previous: 2.1 解答 索引
2.2
1.
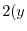 |
 |
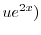 |
|
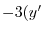 |
 |
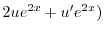 |
|
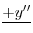 |
 |
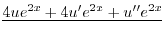 |
|
| 0 |  |
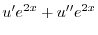 |
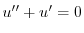
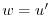 とおくと
とおくと
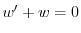
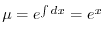 より,これを両辺にかけて
より,これを両辺にかけて
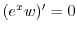 を得る.これを解くと
を得る.これを解くと
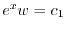 より
より
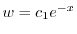
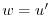 に注意すると
に注意すると
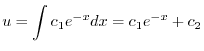
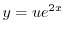 であることに注意して次の一般解を得る.
であることに注意して次の一般解を得る.
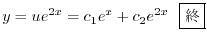
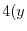 |
 |
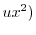 |
|
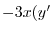 |
 |
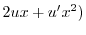 |
|
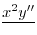 |
 |
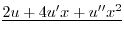 |
|
| 0 |  |
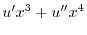 |
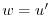 とおくと
とおくと
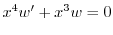
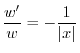
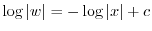 .よって
.よって
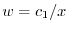 となる.
ここで
となる.
ここで
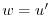 に注意すると
に注意すると
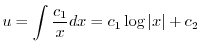
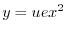 であることに注意すると次の一般解を得る.
であることに注意すると次の一般解を得る.
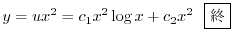
 |
 |
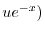 |
|
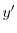 |
 |
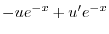 |
|
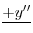 |
 |
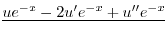 |
|
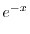 |
 |
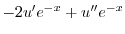 |
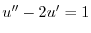
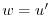 とおくと
とおくと
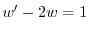
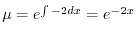 となる.これを両辺にかけると左辺は必ず積分因子かける従属変数の導関数より
となる.これを両辺にかけると左辺は必ず積分因子かける従属変数の導関数より
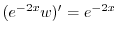
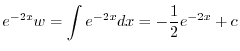
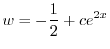
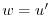 に注意すると
に注意すると
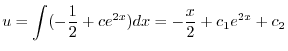
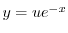 であることに注意して次の一般解を得る.
であることに注意して次の一般解を得る.
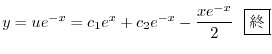
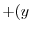 |
 |
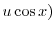 |
|
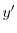 |
 |
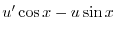 |
|
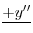 |
 |
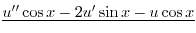 |
|
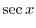 |
 |
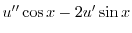 |
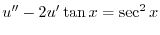
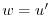 とおくと
とおくと
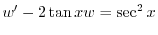
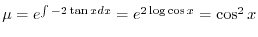 となる.これを両辺にかけると左辺は必ず積分因子かける従属変数の導関数より
となる.これを両辺にかけると左辺は必ず積分因子かける従属変数の導関数より
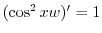 を得る.これを解くと
を得る.これを解くと
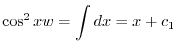
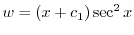
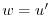 に注意すると
に注意すると
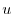 |
 |
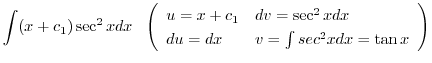 |
|
 |
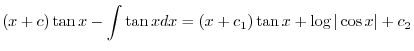 |
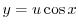 であることに注意して次の一般解を得る.
であることに注意して次の一般解を得る.
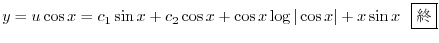
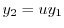 とおくと
とおくと
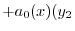 |
 |
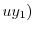 |
|
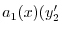 |
 |
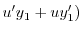 |
|
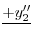 |
 |
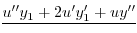 |
|
| 0 |  |
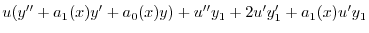 |
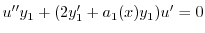
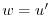 とおくと
とおくと
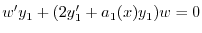
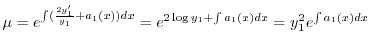
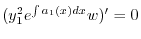
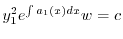
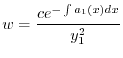
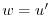 に注意すると
に注意すると
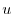 |
 |
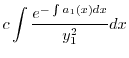 |
|
 |
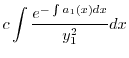 |
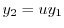 より
より