Next: 7.3.2 Up: 演習問題解答 Previous: 7.2 解答 索引
7.3.1
変数分離法を用いる.
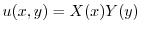 とおき,Laplace方程式に代入すると
とおき,Laplace方程式に代入すると
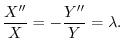
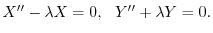
 の境界条件を用いると,すべての
の境界条件を用いると,すべての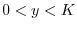 に対して
に対して
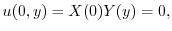
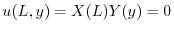
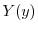 が0でないならば,
が0でないならば,
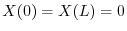 を意味する.よってこれよりSturm-Liouville問題
を意味する.よってこれよりSturm-Liouville問題
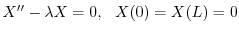
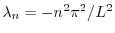 ,固有関数
,固有関数
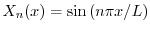 を持っている.さらに,固有値が
を持っている.さらに,固有値が
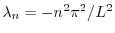 のとき,
のとき,
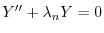
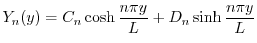
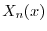 と
と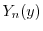 の積
の積
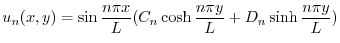
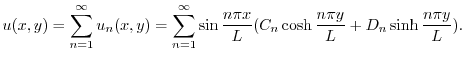
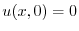 より,
より,
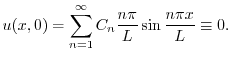
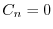 .最後に境界条件
.最後に境界条件
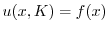 より
より
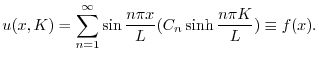
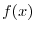 に収束するように
に収束するように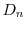 を選ばなければならない.ところがこれは皆さんがよく知っている関数
を選ばなければならない.ところがこれは皆さんがよく知っている関数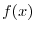 の
の![$[0,L]$](img2666.png) でのフーリエ正弦級数展開である.よって
でのフーリエ正弦級数展開である.よって
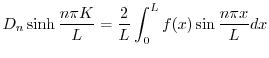
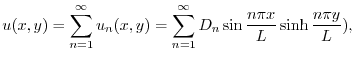
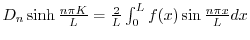 .
.

2.
(a) 変数分離法を用いる.
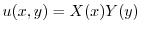 とおき,Laplace方程式に代入すると
とおき,Laplace方程式に代入すると
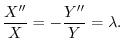
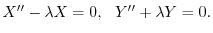
 の境界条件を用いると,すべての
の境界条件を用いると,すべての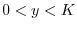 に対して
に対して
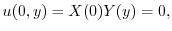
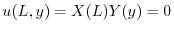
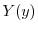 が0でないならば,
が0でないならば,
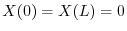 を意味する.よってこれよりSturm-Liouville問題
を意味する.よってこれよりSturm-Liouville問題
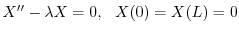
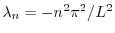 ,固有関数
,固有関数
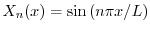 を持っている.さらに,固有値が
を持っている.さらに,固有値が
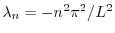 のとき,
のとき,
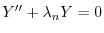
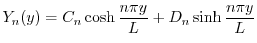
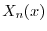 と
と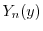 の積
の積
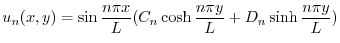
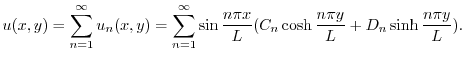
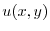 が
が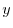 について項別微分可能であるとすると,初期条件
について項別微分可能であるとすると,初期条件
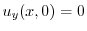 より,
より,
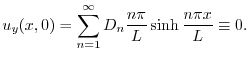
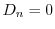 .最後に境界条件
.最後に境界条件
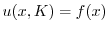 より
より
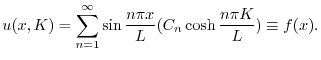
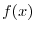 に収束するように
に収束するように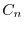 を選ばなければならない.ところがこれは関数
を選ばなければならない.ところがこれは関数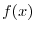 の
の![$[0,L]$](img2666.png) でのフーリエ正弦級数展開である.よって
でのフーリエ正弦級数展開である.よって
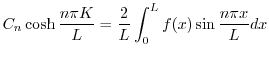
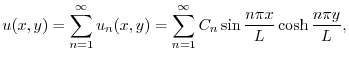
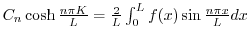 .
.

(b) 変数分離法を用いる.
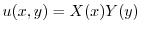 とおき,Laplace方程式に代入すると
とおき,Laplace方程式に代入すると
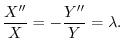
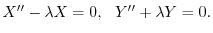
 の境界条件を用いると,すべての
の境界条件を用いると,すべての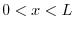 に対して
に対して
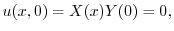
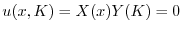
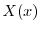 が0でないならば,
が0でないならば,
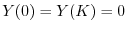 を意味する.よってこれよりSturm-Liouville問題
を意味する.よってこれよりSturm-Liouville問題
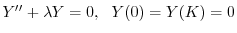
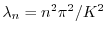 ,固有関数
,固有関数
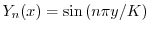 を持っている.さらに,固有値が
を持っている.さらに,固有値が
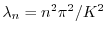 のとき,
のとき,
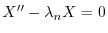
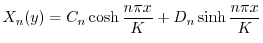
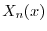 と
と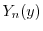 の積
の積
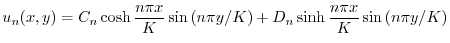
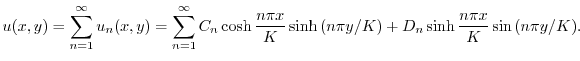
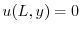 より
より
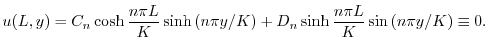
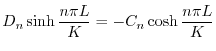
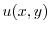 |
 |
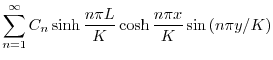 |
|
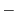 |
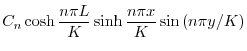 |
||
 |
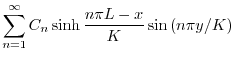 |
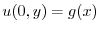 より,
より,
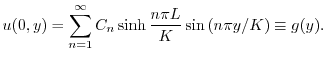
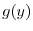 に収束するように
に収束するように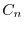 を選ばなければならない.ところがこれは関数
を選ばなければならない.ところがこれは関数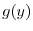 の
の![$[0,K]$](img2699.png) でのフーリエ正弦級数展開である.よって
でのフーリエ正弦級数展開である.よって
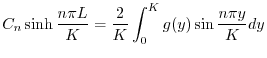
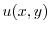 |
 |
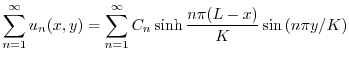 |
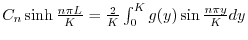 .
.

3. 変数分離法を用いる.
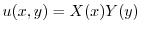 とおき,Laplace方程式に代入すると
とおき,Laplace方程式に代入すると
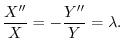
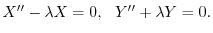
 の境界条件を用いると,すべての
の境界条件を用いると,すべての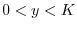 に対して
に対して
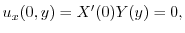
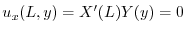
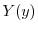 が0でないならば,
が0でないならば,
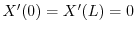 を意味する.よってこれより
を意味する.よってこれより
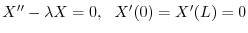
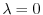 のとき
のとき
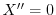 より
より
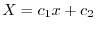 .ここで境界値
.ここで境界値
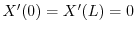 を用いると
を用いると
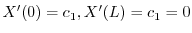
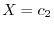 .
.
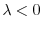 のとき,
のとき,
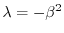 とおくと,
とおくと,
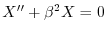
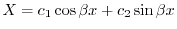 .ここで境界値
.ここで境界値
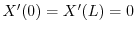 を用いると
を用いると
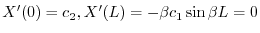
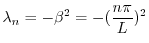
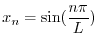
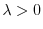 のとき,
のとき,
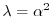 とおくと,
とおくと,
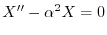
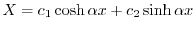 .ここで境界値
.ここで境界値
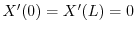 を用いると
を用いると
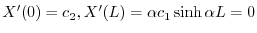
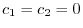 .これより
固有値
.これより
固有値
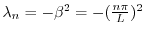 ,固有関数
,固有関数
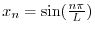 を得る.
を得る.
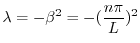
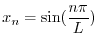
より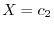 .
この問題は固有値
.
この問題は固有値
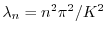 ,固有関数
,固有関数
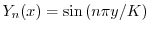 を持っている.さらに,固有値が
を持っている.さらに,固有値が
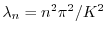 のとき,
のとき,
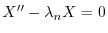
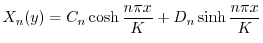
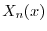 と
と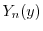 の積
の積
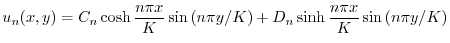
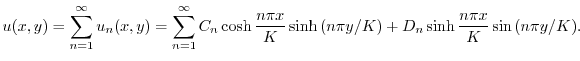
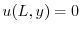 より
より
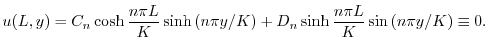
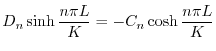
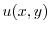 |
 |
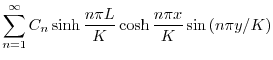 |
|
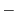 |
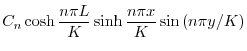 |
||
 |
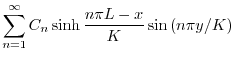 |
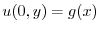 より,
より,
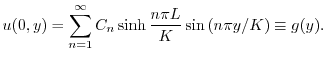
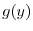 に収束するように
に収束するように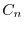 を選ばなければならない.ところがこれは関数
を選ばなければならない.ところがこれは関数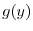 の
の![$[0,K]$](img2699.png) でのフーリエ正弦級数展開である.よって
でのフーリエ正弦級数展開である.よって
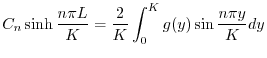
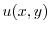 |
 |
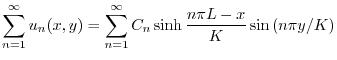 |
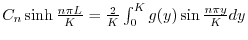 .
.
