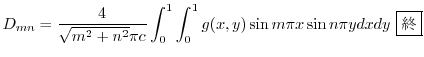Next: 7.3.3 解答 Up: 演習問題解答 Previous: 7.3.1 解答 索引
7.3.2
1.
(a) まず弾性弦の垂直方向の変位を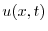 とすると,
とすると,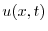 は一次元波動方程式
は一次元波動方程式
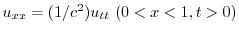 を満たす.次に,初期条件は
を満たす.次に,初期条件は
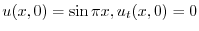
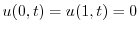
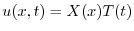 とおき,一次元波動方程式に代入すると
とおき,一次元波動方程式に代入すると
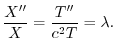
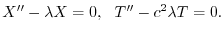
 の境界条件を用いると,すべての
の境界条件を用いると,すべての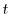 に対して
に対して
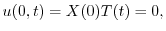
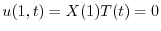
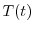 が0でないならば,
が0でないならば,
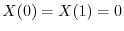 を意味する.よってこれよりSturm-Liouville問題
を意味する.よってこれよりSturm-Liouville問題
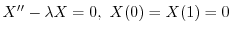
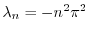 ,固有関数
,固有関数
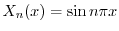 をもっている.また,固有値
をもっている.また,固有値
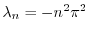 のとき,
のとき,
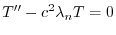
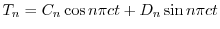
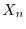 と
と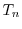 の積
の積
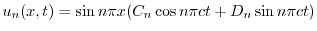
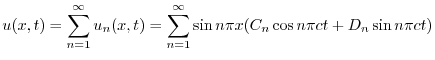
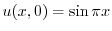 より
より
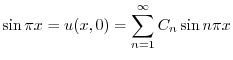
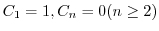 .次に
.次に
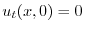 より
より
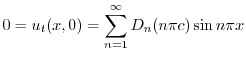
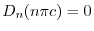 .よって
.よって
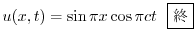
(b) まず弾性弦の垂直方向の変位を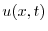 とすると,
とすると,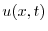 は一次元波動方程式
は一次元波動方程式
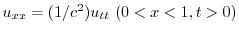 を満たす.次に,初期条件は初速度1m/secより
を満たす.次に,初期条件は初速度1m/secより
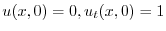
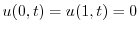
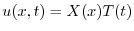 とおき,一次元波動方程式に代入すると
とおき,一次元波動方程式に代入すると
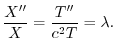
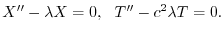
 の境界条件を用いると,すべての
の境界条件を用いると,すべての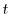 に対して
に対して
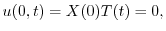
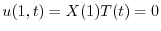
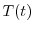 が0でないならば,
が0でないならば,
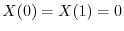 を意味する.よってこれよりSturm-Liouville問題
を意味する.よってこれよりSturm-Liouville問題
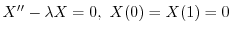
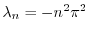 ,固有関数
,固有関数
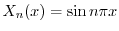 をもっている.また,固有値
をもっている.また,固有値
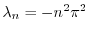 のとき,
のとき,
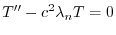
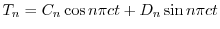
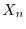 と
と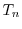 の積
の積
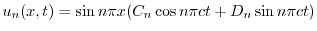
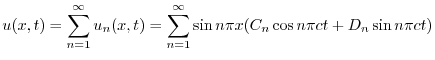
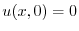 より
より
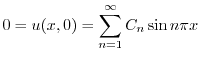
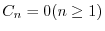 .次に
.次に
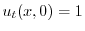 より
より
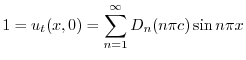
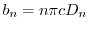 とおくと
とおくと
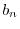 |
 |
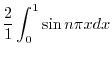 |
|
 |
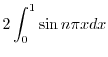 |
||
 |
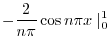 |
||
 |
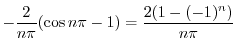 |
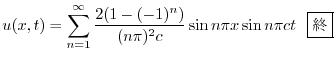
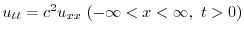 において,
において,
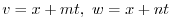 とおくと
とおくと
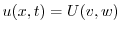 より
より
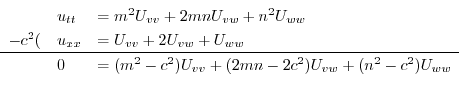
ここで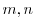 を
を
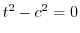 の解とすると
の解とすると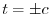 .
よって
.
よって
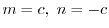 とおくと
とおくと
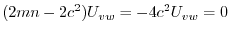
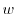 について積分すると
について積分すると
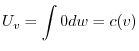
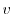 について積分すると
について積分すると
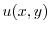 |
 |
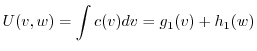 |
|
 |
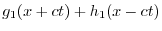 |
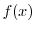 |
 |
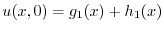 |
|
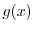 |
 |
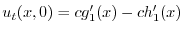 |
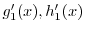 を求めると,
を求めると,
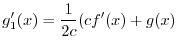
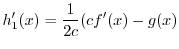
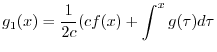
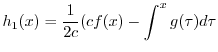
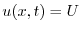 |
 |
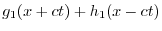 |
|
 |
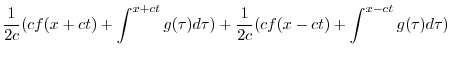 |
||
 |
![$\displaystyle \frac{1}{2}[f(x + ct) + g(x - ct)] + \frac{1}{2c}\int_{x-ct}^{x+ct}g(\tau)d\tau \ \framebox{終}$](img2782.png) |
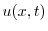 |
 |
![$\displaystyle \frac{1}{2}[e^{-(x+ct)^2} + e^{-(x-ct)^{2}}] + \frac{1}{2c}\int_{x-ct}^{x+ct}d\tau$](img2786.png) |
|
 |
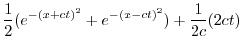 |
||
 |
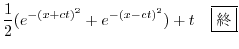 |
4.
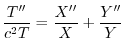
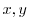 と独立で,右辺は
と独立で,右辺は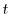 と独立なので,両辺とも定数となり,この定数を
と独立なので,両辺とも定数となり,この定数を
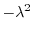 とおくと
とおくと
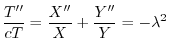
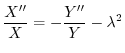
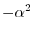 とおくと,次の3つの微分方程式を得る.
とおくと,次の3つの微分方程式を得る.
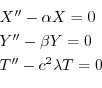
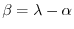 .ここで境界条件
.ここで境界条件
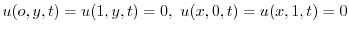
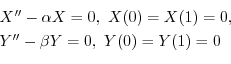
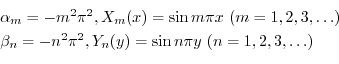
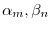 に対して,
に対して,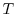 は
は
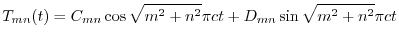
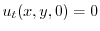 より
より
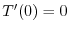 となるので
となるので
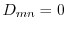 ,よって
,よって
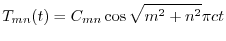
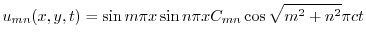
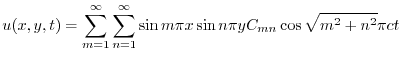
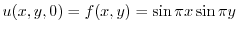 より
より
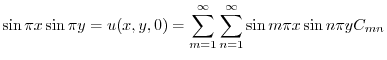
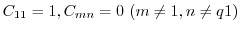 .これより
.これより
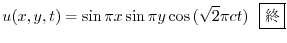
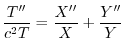
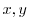 と独立で,右辺は
と独立で,右辺は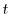 と独立なので,両辺とも定数となり,この定数を
と独立なので,両辺とも定数となり,この定数を
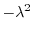 とおくと
とおくと
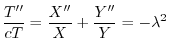
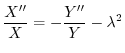
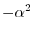 とおくと,次の3つの微分方程式を得る.
とおくと,次の3つの微分方程式を得る.
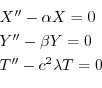
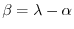 .ここで境界条件
.ここで境界条件
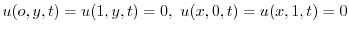
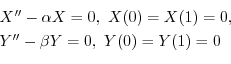
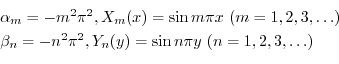
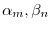 に対して,
に対して,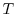 は
は
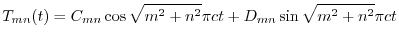
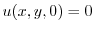 より
より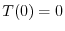 となるので
となるので
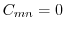 ,よって
,よって
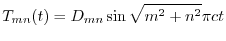
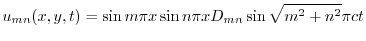
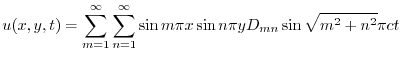
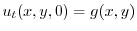 より
より
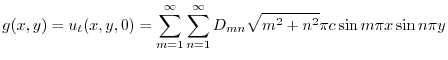
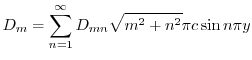
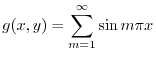
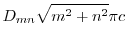 |
 |
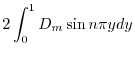 |
|
 |
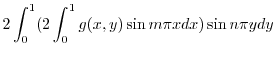 |
||
 |
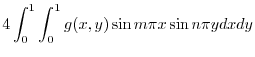 |