Next: 7.3.1 解答 Up: 演習問題解答 Previous: 7.1 解答 索引
7.2
1.
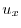 |
 |
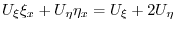 |
|
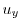 |
 |
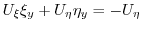 |
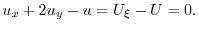
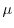 を求めると
を求めると
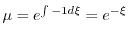
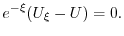
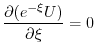
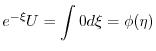
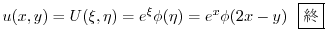
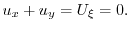
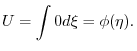
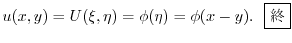
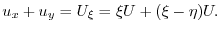
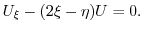
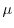 を求めると
を求めると
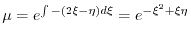
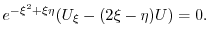
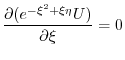
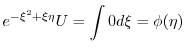
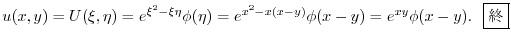
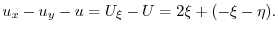
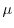 を求めると
を求めると
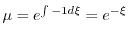
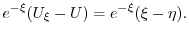
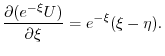
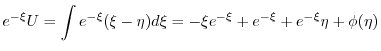
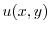 |
 |
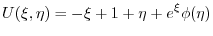 |
|
 |
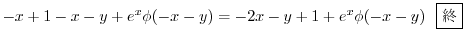 |
2.
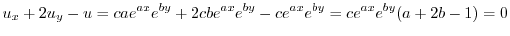
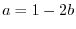 とおくと,どんな
とおくと,どんな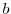 に対しても
に対しても
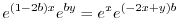 は解になるので,任意の関数
は解になるので,任意の関数
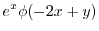 をもちいて表わすと
をもちいて表わすと
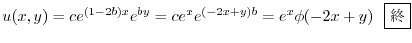
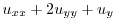 |
 |
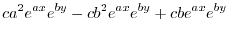 |
|
 |
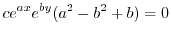 |
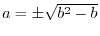 .
.
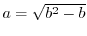 とおくと,どんな
とおくと,どんな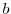 に対しても
に対しても
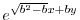 は解.また
は解.また
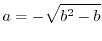 とおくと,どんな
とおくと,どんな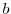 に対しても
に対しても
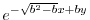 は解である.解の1次結合はまた解なので任意の関数
は解である.解の1次結合はまた解なので任意の関数 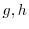 を用いて
を用いて
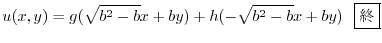
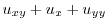 |
 |
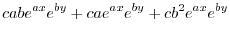 |
|
 |
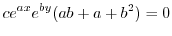 |
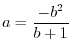 と表わせるので
と表わせるので
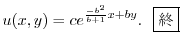
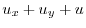 |
 |
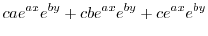 |
|
 |
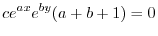 |
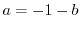 と表わせるので
と表わせるので
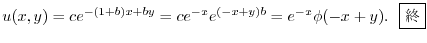
3.
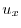 |
 |
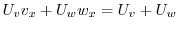 |
|
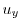 |
 |
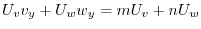 |
|
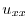 |
 |
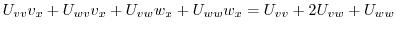 |
|
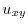 |
 |
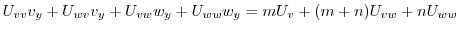 |
|
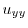 |
 |
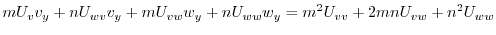 |
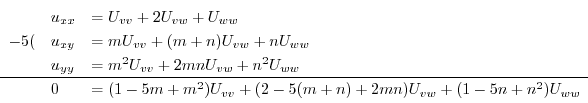
ここで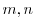 を
を
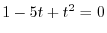 の解とすると
の解とすると
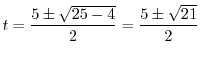
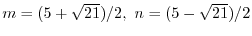 とおくと
とおくと
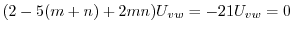
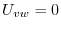 となるので
となるので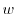 について積分すると
について積分すると
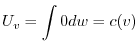
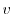 について積分すると
について積分すると
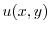 |
 |
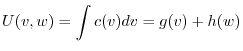 |
|
 |
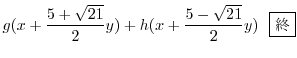 |
ここで を
を
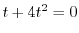 の解とすると
の解とすると
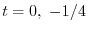 .
よって
.
よって
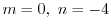 とおくと
とおくと
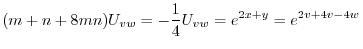
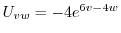 となるので
となるので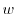 について積分すると
について積分すると
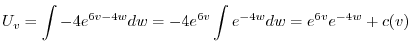
 について積分すると
について積分すると
 |
 |
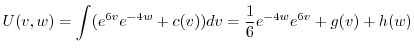 |
|
 |
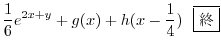 |
ここで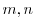 を
を
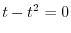 の解とすると
の解とすると
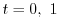 .
よって
.
よって
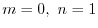 とおくと
とおくと
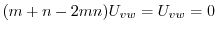
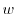 について積分すると
について積分すると
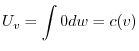
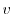 について積分すると
について積分すると
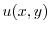 |
 |
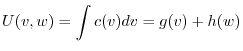 |
|
 |
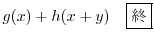 |
ここで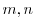 を
を
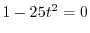 の解とすると
の解とすると
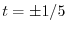 .
よって
.
よって
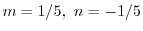 とおくと
とおくと
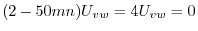
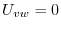 となるので
となるので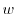 について積分すると
について積分すると
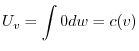
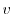 について積分すると
について積分すると
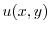 |
 |
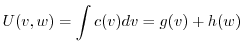 |
|
 |
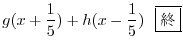 |