Next: 3.3 解答 Up: 演習問題解答 Previous: 3.1 解答 索引
3.2
1.
(a)
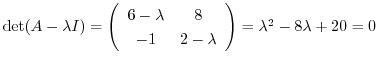 .
よって固有値は
.
よって固有値は
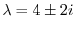 である.次に固有値
である.次に固有値
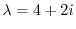 に対する固有ベクトル
に対する固有ベクトル は
は
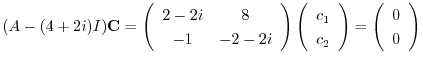
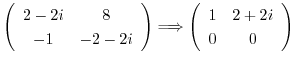 は被約階段行列に変形されるので,
は被約階段行列に変形されるので,
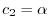 とおくと,
とおくと,
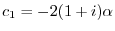 となる.したがって,固有ベクトルは
となる.したがって,固有ベクトルは
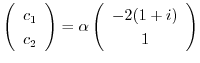 である.これより
である.これより
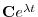 の実部と虚部を求めると
の実部と虚部を求めると
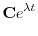 |
 |
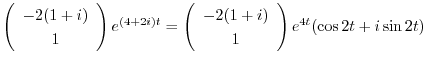 |
|
 |
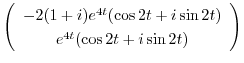 |
||
 |
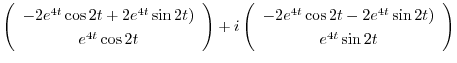 |
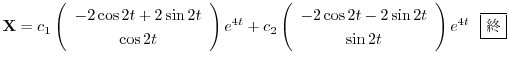
(b)
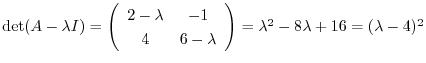 より固有値は
より固有値は
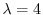 である.次に固有値
である.次に固有値
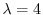 に対する固有ベクトル
に対する固有ベクトル は
は
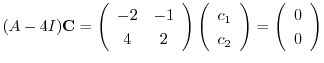
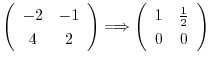
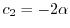 とおくと,
とおくと,
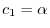 となる.したがって,固有ベクトルは
となる.したがって,固有ベクトルは
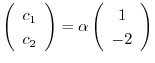 である.次に,
である.次に,
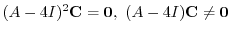
 を見つけると
を見つけると
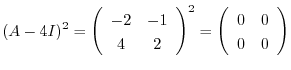
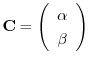 は
は
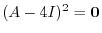 を満たす.ここでもう一つの条件を満たすように
を満たす.ここでもう一つの条件を満たすように
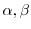 を選ぶと,
を選ぶと,
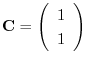 となり,2つめの解
となり,2つめの解
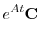 |
 |
![$\displaystyle e^{4t}e^{(A-4I)t}{\bf C} = e^{4t}[{\bf C} + t(A - 4I){\bf C} + \frac{t^2}{2!}(A - 4I)^2 {\bf C}]$](img1464.png) |
|
 |
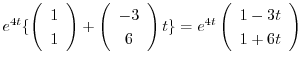 |
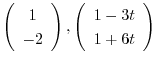 は1次独立なので,一般解は次のように表わすことができる.
は1次独立なので,一般解は次のように表わすことができる.
![$\displaystyle {\bf X} =e^{4t}[c_{1}\left(\begin{array}{c}
1\\
-2
\end{array...
...c_{2}\left(\begin{array}{c}
1-3t\\
1+6t
\end{array}\right)] \ \framebox{終} $](img1467.png)
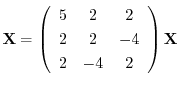 より
より
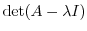 |
 |
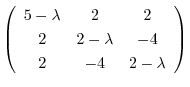 |
|
 |
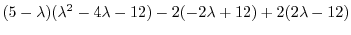 |
||
 |
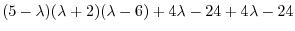 |
||
 |
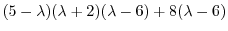 |
||
 |
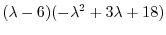 |
||
 |
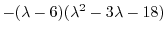 |
||
 |
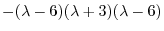 |
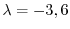 である.
である.
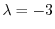 に対する固有ベクトル
に対する固有ベクトル は
は
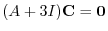 の0でない解より,Gaussの消去法を用いて求める.
の0でない解より,Gaussの消去法を用いて求める.
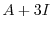 |
 |
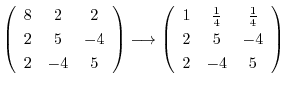 |
|
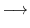 |
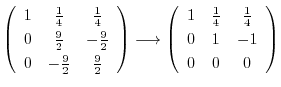 |
||
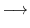 |
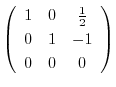 |
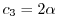 とおくと,
とおくと,
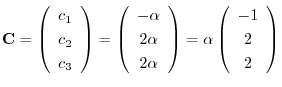
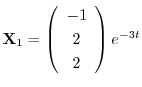 を得る.
を得る.
次に,固有値
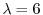 に対する固有ベクトルを求める.
に対する固有ベクトルを求める.
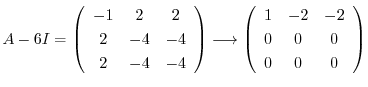
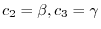 とおくと,
とおくと,
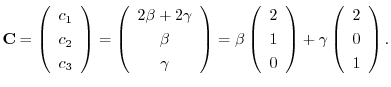
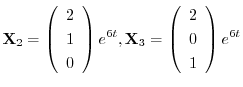
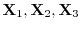 は互いに1次独立なので,一般解は
は互いに1次独立なので,一般解は
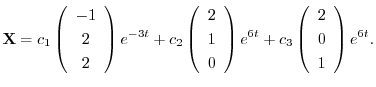

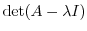 |
 |
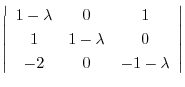 |
|
 |
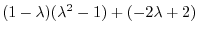 |
||
 |
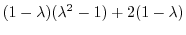 |
||
 |
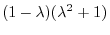 |
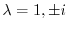 を得る.
を得る.
固有値
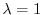 に対する固有ベクトル
に対する固有ベクトル をGaussの消去法を用いて求める.
をGaussの消去法を用いて求める.
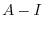 |
 |
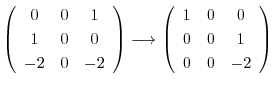 |
|
 |
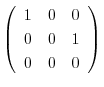 |
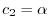 とおくと,
とおくと,
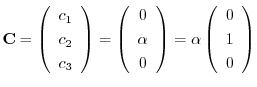
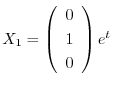 を得る.
を得る.
次に
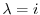 に対する固有ベクトル
に対する固有ベクトル を求める.
を求める.
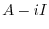 |
 |
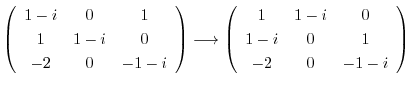 |
|
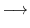 |
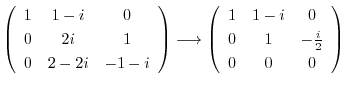 |
||
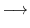 |
 |
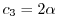 とおくと,
とおくと,
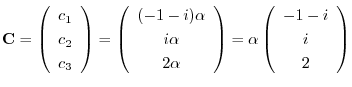
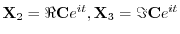 で与えられるので,
で与えられるので,
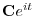 の実部と虚部を求める.
の実部と虚部を求める.
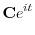 |
 |
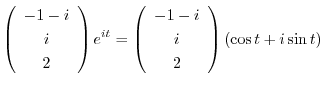 |
|
 |
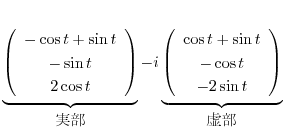 |
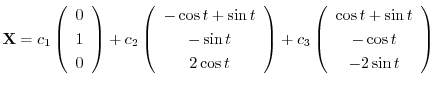

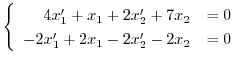
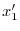 について解くと,
について解くと,
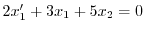 より
より
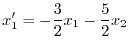 |
(A.8) |
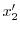 について解くと,
について解くと,
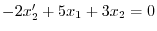 より
より
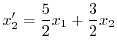 |
(A.9) |
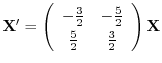
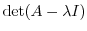 |
 |
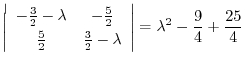 |
|
 |
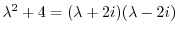 |
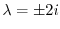 .
.
固有値
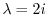 に対する固有ベクトルをGaussの消去法を用いて求める.
に対する固有ベクトルをGaussの消去法を用いて求める.
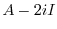 |
 |
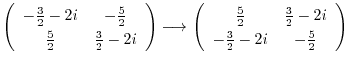 |
|
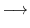 |
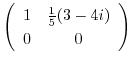 |
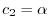 とおくと,
とおくと,
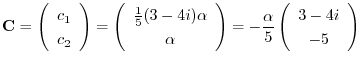
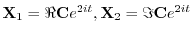 を求める.
を求める.
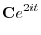 |
 |
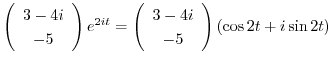 |
|
 |
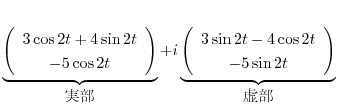 |
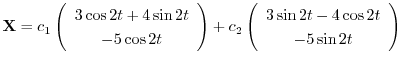

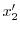 について解くと,
について解くと,
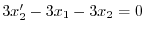 より
より
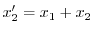
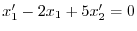 より
より
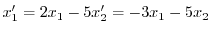
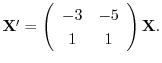 となる.これより固有値と固有ベクトルを求める.
となる.これより固有値と固有ベクトルを求める.
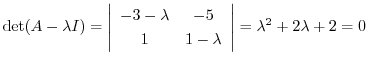
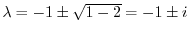 を得る.
を得る.
固有値
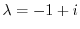 に対する固有ベクトル
に対する固有ベクトル をGaussの消去法を用いて求める.
をGaussの消去法を用いて求める.
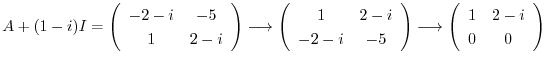
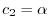 とおくと,
とおくと,
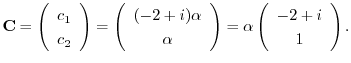
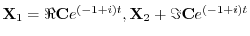 を求める.
を求める.
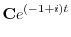 |
 |
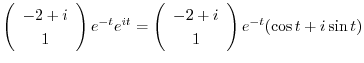 |
|
 |
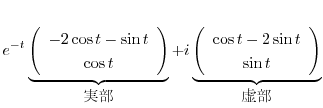 |
![$\displaystyle {\bf X} = e^{-t}[c_{1}\left(\begin{array}{c}
-2\cos{t}-\sin{t}\\ ...
...+ c_{2} \left(\begin{array}{c}
\cos{t}-2\sin{t}\\
\sin{t}
\end{array}\right)] $](img1550.png)
