Next: 4.1 解答 Up: 演習問題解答 Previous: 3.2 解答 索引
3.3
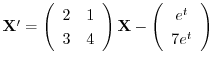 よりまず
よりまず
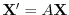 の解
の解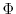 を求める.
を求める.
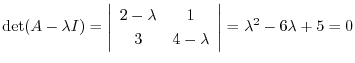
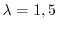 を得る.
を得る.
固有値
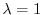 に対する固有ベクトル
に対する固有ベクトル をGaussの消去法を用いて求める.
をGaussの消去法を用いて求める.
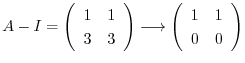
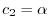 とおくと
とおくと
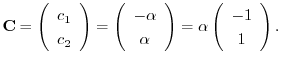
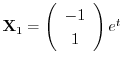 を得る.
を得る.
固有値
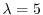 に対する固有ベクトル
に対する固有ベクトル は
は
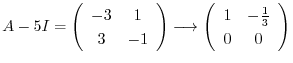
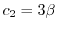 とおくと
とおくと
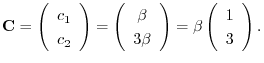
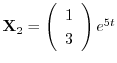 を得る.これより基本行列
を得る.これより基本行列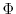 は
は
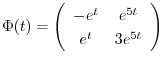
次に
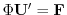 を解き特殊解
を解き特殊解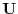 を求める.
を求める.
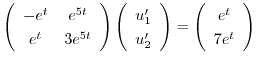
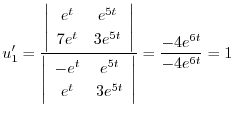
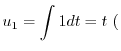 特殊解を求めるので積分定数をつけない
特殊解を求めるので積分定数をつけない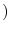
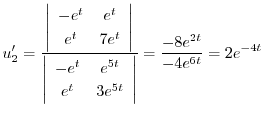
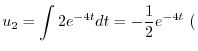 特殊解を求めるので積分定数をつけない
特殊解を求めるので積分定数をつけない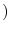
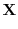 |
 |
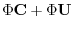 |
|
 |
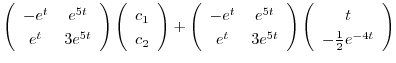 |

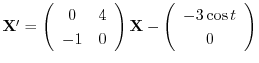 よりまず
よりまず
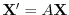 の解
の解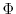 を求める.
を求める.
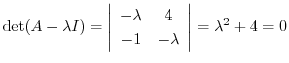
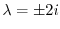 を得る.
を得る.
固有値
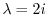 に対する固有ベクトル
に対する固有ベクトル をGaussの消去法を用いて求める.
をGaussの消去法を用いて求める.
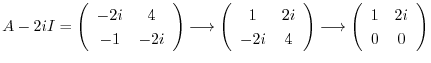
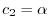 とおくと
とおくと
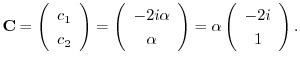
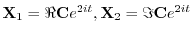 を得る.ここで
を得る.ここで
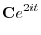 |
 |
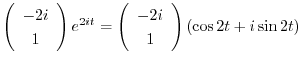 |
|
 |
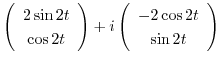 |
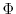 は
は
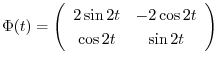
次に
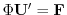 を解き特殊解
を解き特殊解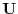 を求める.
を求める.
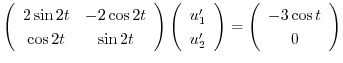
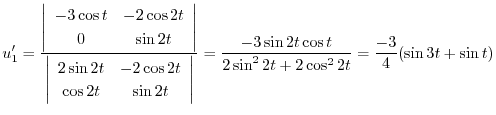
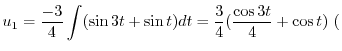 積分定数をつけない
積分定数をつけない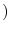
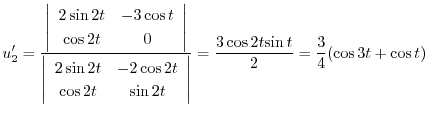
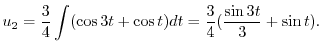
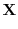 |
 |
 |
|
 |
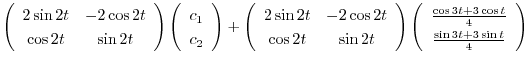 |

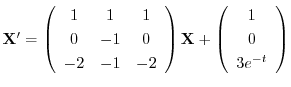 よりまず
よりまず
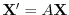 の解
の解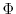 を求める.
を求める.
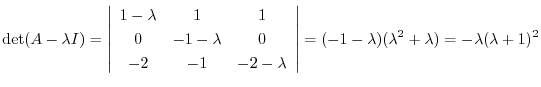
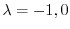 を得る.
を得る.
固有値
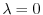 に対する固有ベクトル
に対する固有ベクトル をGaussの消去法を用いて求める.
をGaussの消去法を用いて求める.
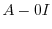 |
 |
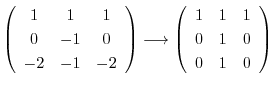 |
|
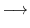 |
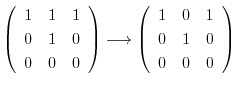 |
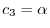 とおくと,
とおくと,
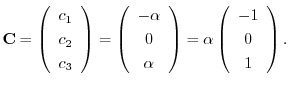
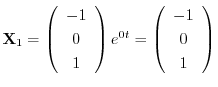 を得る.
を得る.
固有値
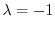 に対する固有ベクトル
に対する固有ベクトル を求める.
を求める.
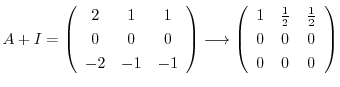
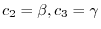 とおくと,
とおくと,
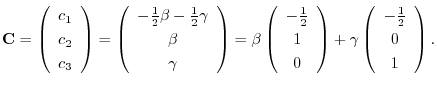
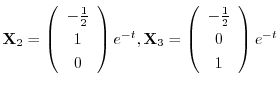 を得る.これより基本行列
を得る.これより基本行列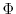 は
は
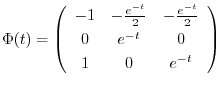
次に
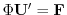 より特殊解
より特殊解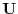 を求める.
を求める.
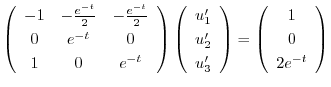
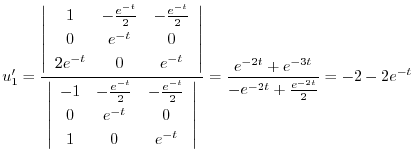
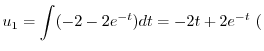 特殊解を求めるので積分定数をつけない
特殊解を求めるので積分定数をつけない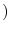
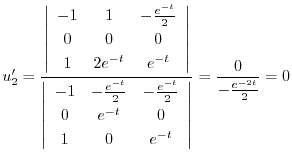
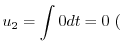 特殊解を求めるので積分定数をつけない
特殊解を求めるので積分定数をつけない
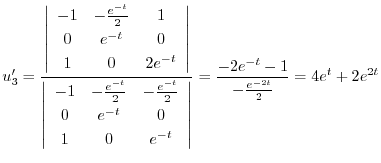
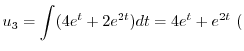 特殊解を求めるので積分定数をつけない
特殊解を求めるので積分定数をつけない
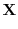 |
 |
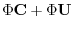 |
|
 |
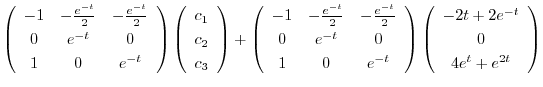 |

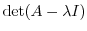 |
 |
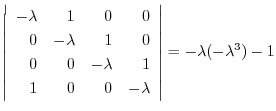 |
|
 |
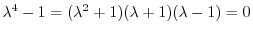 |
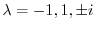 を得る.
を得る.
固有値
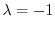 に対する固有ベクトル
に対する固有ベクトル をGaussの消去法を用いて求める.
をGaussの消去法を用いて求める.
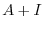 |
 |
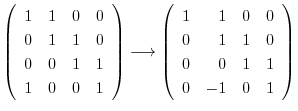 |
|
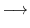 |
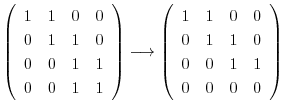 |
||
 |
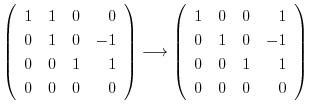 |
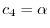 とおくと,
とおくと,
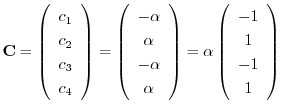
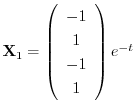 を得る.
を得る.
固有値
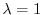 に対する固有ベクトル
に対する固有ベクトル を求める.
を求める.
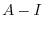 |
 |
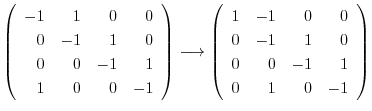 |
|
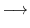 |
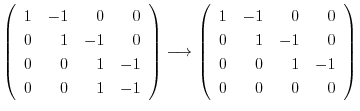 |
||
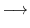 |
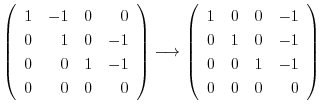 |
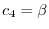 とおくと,
とおくと,
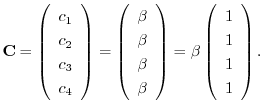
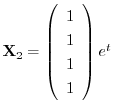 を得る.
を得る.
固有値
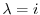 に対する固有ベクトル
に対する固有ベクトル を求める.
を求める.
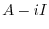 |
 |
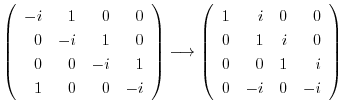 |
|
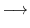 |
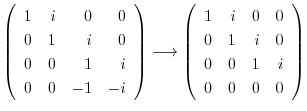 |
||
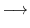 |
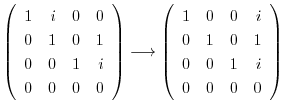 |
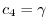 とおくと,
とおくと,
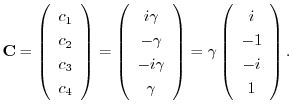
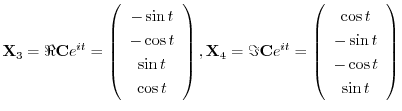
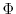 は
は
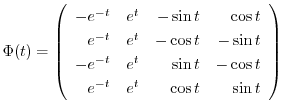
次に,
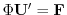 より特殊解
より特殊解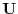 を求める.
を求める.
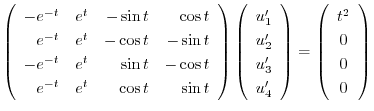
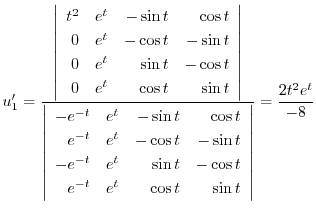
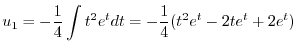
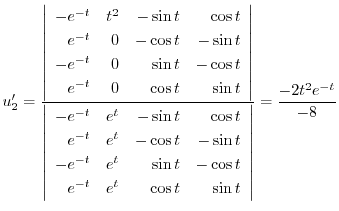
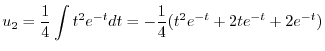
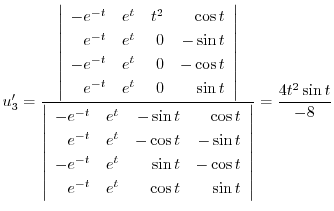
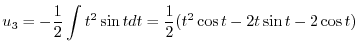
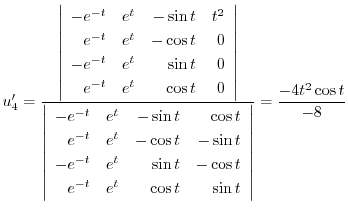
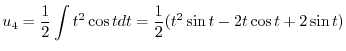
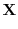 |
 |
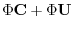 |
|
 |
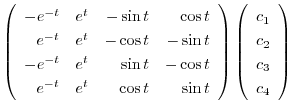 |
||
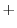 |
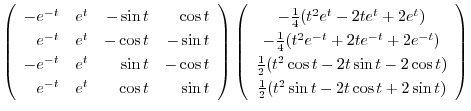 |

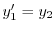 とおくと,
とおくと,
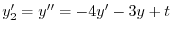 .よって
.よって
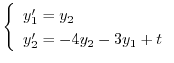
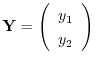 とおくと,
とおくと,
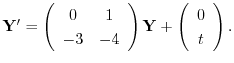
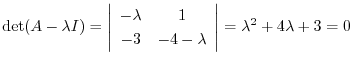
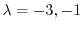 を得る.
を得る.
固有値
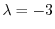 に対する固有ベクトル
に対する固有ベクトル をGaussの消去法を用いて求める.
をGaussの消去法を用いて求める.
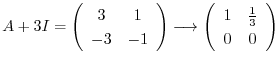
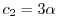 とおくと,
とおくと,
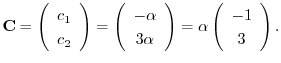
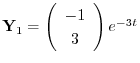 を得る.
を得る.
固有値
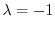 に対する固有ベクトル
に対する固有ベクトル をGaussの消去法を用いて求める.
をGaussの消去法を用いて求める.
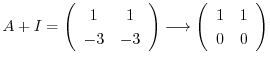
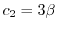 とおくと,
とおくと,
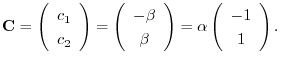
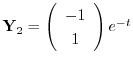 を得る.これより基本行列
を得る.これより基本行列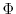 は
は
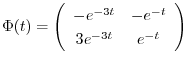
次に,
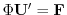 より特殊解
より特殊解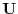 を求める.
を求める.
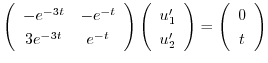
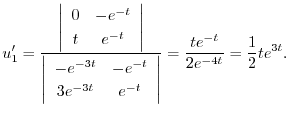
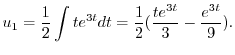
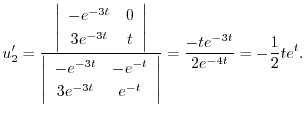
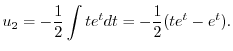
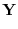 |
 |
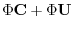 |
|
 |
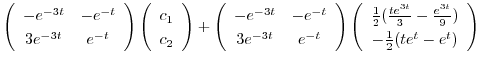 |

3.
より
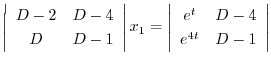
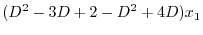 |
 |
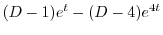 |
|
 |
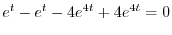 |
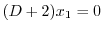
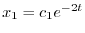 .同様にして
.同様にして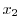 を求めることができるが,一般に
を求めることができるが,一般に
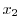 を求めるには,A.10の式から
を求めるには,A.10の式から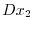 を消去してそこに
を消去してそこに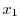 を代入する方が簡単である.実際にやってみるとA.10の最初の式から次の式を引くと,
を代入する方が簡単である.実際にやってみるとA.10の最初の式から次の式を引くと,
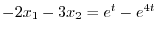 を得る.よって
を得る.よって
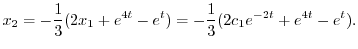
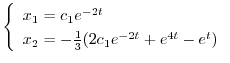

より
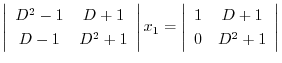
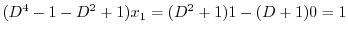
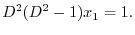
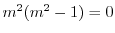 より,
より,
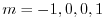 .
よって余関数は
.
よって余関数は
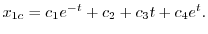
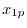 を未定係数法で求める.
を未定係数法で求める.
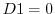 より
より
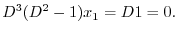
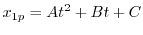
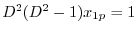 より,
より,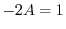 .よって
.よって
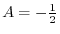 .これより,
.これより,
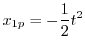
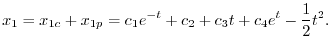
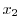 を求める.A.11の式からまず.
を求める.A.11の式からまず.
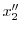 を消去すると
を消去すると
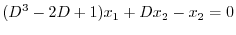
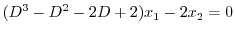
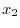 |
 |
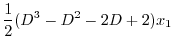 |
|
 |
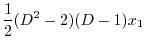 |
||
 |
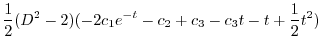 |
||
 |
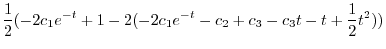 |
||
 |
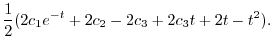 |
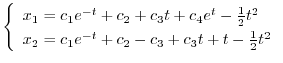

より
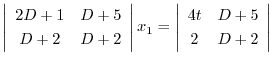
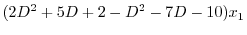 |
 |
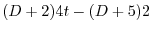 |
|
 |
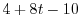 |
||
 |
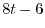 |
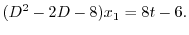
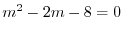 より,
より,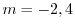 .
よって余関数は
.
よって余関数は
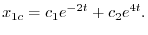
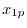 を未定係数法で求める.
を未定係数法で求める.
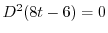 より
より
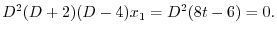
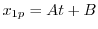
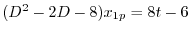 より,
より,
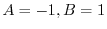 .これより,
.これより,
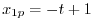
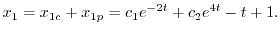
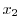 を求める.A.12の式からまず.
を求める.A.12の式からまず.
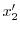 を消去すると
を消去すると
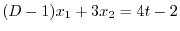
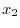 |
 |
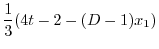 |
|
 |
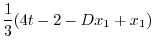 |
||
 |
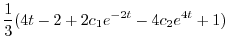 |
||
 |
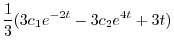 |
||
 |
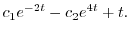 |
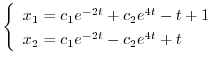

より
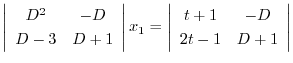
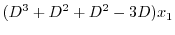 |
 |
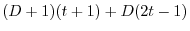 |
|
 |
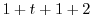 |
||
 |
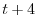 |
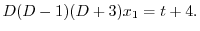
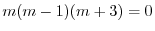 より,
より,
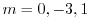 .
よって余関数は
.
よって余関数は
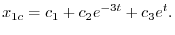
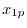 を未定係数法で求める.
を未定係数法で求める.
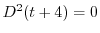 より
より
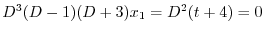 .このうち,
.このうち,
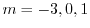 は余関数に用いられているので,
は余関数に用いられているので,
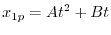
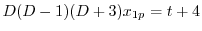 より,
より,
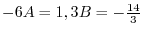 .これより,
.これより,
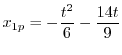
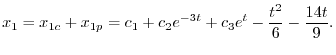
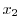 を求める.A.13の式からまず.
を求める.A.13の式からまず.
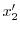 を消去すると
を消去すると
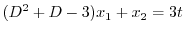
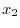 |
 |
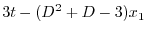 |
|
 |
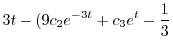 |
||
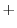 |
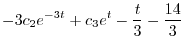 |
||
 |
 |
||
 |
 |