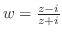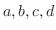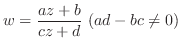Next: 1次分数関数(linear fractional transformation) Up: 複素関数 Previous: 複素関数 索引
 の各点
の各点
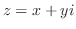 に対し,1つの複素数
に対し,1つの複素数
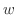 ,
,
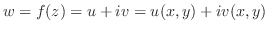 が対応するとき,
が対応するとき, を領域
を領域 で定義された複素関数といい,
で定義された複素関数といい,
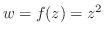 と表わす.この領域
と表わす.この領域 を関数
を関数 の 定義域(domain)という.
の 定義域(domain)という.
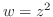
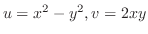
解
(a) 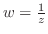 の定義域
の定義域 は全平面で,
は全平面で,
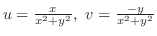
(b)
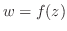 の定義域
の定義域 は原点を除く全平面で,
は原点を除く全平面で,
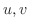
複素関数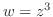 は
は 平面上の点
平面上の点 を
を 平面上の点
平面上の点 に対応させる写像と考えられるから,写像
に対応させる写像と考えられるから,写像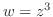 ということもある.このとき
ということもある.このとき を像,
を像, を原像という.
を原像という.
一般には,1つの に対応する
に対応する の値は1つと限らないが,私の講義では特に断らない限り
の値は1つと限らないが,私の講義では特に断らない限り の値がただ1つ対応する1価関数だけを扱う.
の値がただ1つ対応する1価関数だけを扱う.
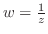 のとき,
のとき,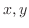 を
を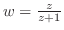 の関数で表し,
の関数で表し,
 平面の実軸および虚軸に平行な
平面の実軸および虚軸に平行な 平面のどのような曲線に写像されるかを調べよ.
平面のどのような曲線に写像されるかを調べよ.
2. 次の関数について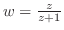 を
を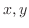 の関数で表せ.
の関数で表せ.