Next: 1次関数 Up: 演習問題詳解 Previous: 1.2 ドゥモワブルの定理とオイラーの公式 索引
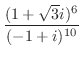
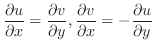 ,
,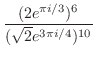 となる.次に,この式を
となる.次に,この式を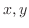 について解く.
について解く.
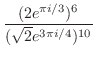 より
より
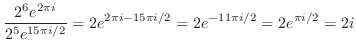 .これを
.これを
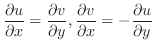 に代入すると
に代入すると
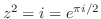
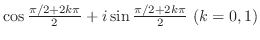 倍すると
倍すると
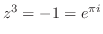
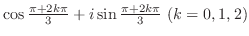 についての2次式と考えることができる.つまり
についての2次式と考えることができる.つまり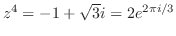 とおく.
よって,解の公式から
とおく.
よって,解の公式から
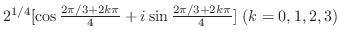
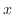 は実部であることに注意すると,
は実部であることに注意すると,
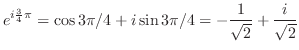
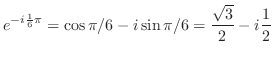
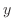 を求める.
を求める.
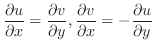 より
より
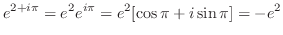
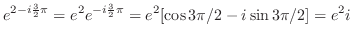
次に 平面の実軸に平行な直線
平面の実軸に平行な直線
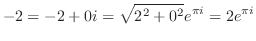 がどんな曲線に写されるか考える.
上の式から
がどんな曲線に写されるか考える.
上の式から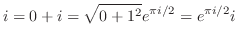 は
は
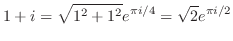
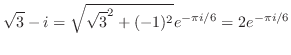
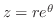 という放物線に写される.
という放物線に写される.
同様に, 平面の虚軸に平行な直線
平面の虚軸に平行な直線
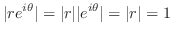 は
は
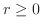
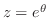
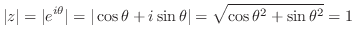 という放物線に写される.
という放物線に写される.
2.
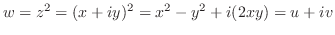
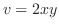 .
.
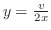
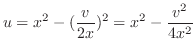 に注意すると
に注意すると
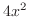
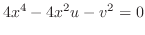 .
.
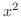
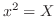 に注意すると
に注意すると
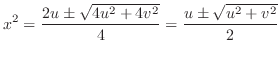
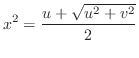 .
.