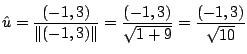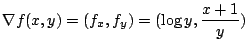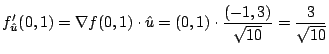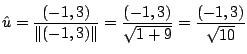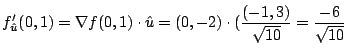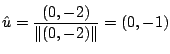Next: 合成関数の偏微分法(differentiation of composite functions Up: 偏微分法(PARTIAL DIFFERENTIATION) Previous: gradientと方向微分(grad and directional derivatives)
6.5
1. 方向微分は
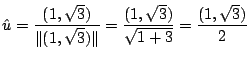
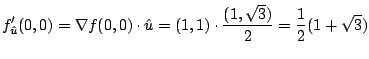
単位方向ベクトル![]() を求めると
を求めると
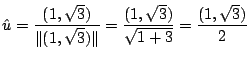
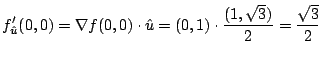
2.
(a)
![]() 方向とは,
方向とは,![]() 軸から
軸から
![]() の方向のことである.そこで,単位方向ベクトル
の方向のことである.そこで,単位方向ベクトル![]() を求めると
を求めると
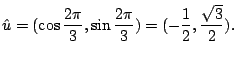
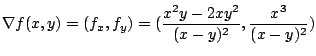
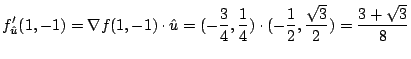
(b)
![]() 方向とは,
方向とは,![]() 軸から
軸から
![]() の方向のことである.そこで,単位方向ベクトル
の方向のことである.そこで,単位方向ベクトル![]() を求めると
を求めると
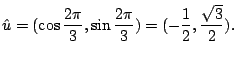
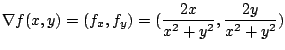
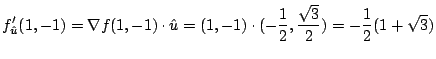
3.