Next: 偏微分(partial derivatives) Up: 偏微分法(PARTIAL DIFFERENTIATION) Previous: 関数の極限(limit of function)
6.2
1.
(a)
![]() は半径1の円を表わし,中心とその外周を含んでいない.したがって,
は半径1の円を表わし,中心とその外周を含んでいない.したがって,![]() の中にどんな点をとってもその近傍が
の中にどんな点をとってもその近傍が![]() に含まれるようにすることができる.よって,
に含まれるようにすることができる.よって,![]() は開集合である.
は開集合である.
![]() は中心を原点とする半径
は中心を原点とする半径![]() の円に含まれるので有界.
の円に含まれるので有界.
![]() に属するどの2点も,
に属するどの2点も,![]() の中だけを通る連続な曲線で結べるので連結.
の中だけを通る連続な曲線で結べるので連結.
連結な開集合を領域というので![]() は領域.
は領域.
Dの境界
![]()
Dの閉領域
![]()
![]() より
より
![]() .
.![]() は開集合なので,
は開集合なので,![]() は閉集合である.
は閉集合である.
どんな半径![]() を持つ開円板
を持つ開円板
![]() にも集合
にも集合![]() は含まれないので非有界.
は含まれないので非有界.
![]() に属するどの2点も,
に属するどの2点も,![]() の中だけを通る連続な曲線で結べるので連結.
の中だけを通る連続な曲線で結べるので連結.
Dの境界
![]()
Dの閉領域
![]()
2.
(a)
分子の項の最小次数![]() 分母の項の最小次数
分母の項の最小次数![]() .よって分母の方が速く0に近づく.そこで,
.よって分母の方が速く0に近づく.そこで,![]() とおくと
とおくと
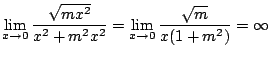
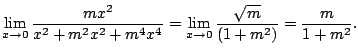
(c)
分子の項の最小次数![]() 分母の項の最小次数
分母の項の最小次数![]() より
より
![]() とおくと
とおくと
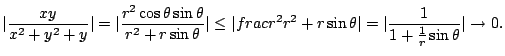
3.
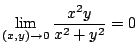
分子の項の最小次数![]() 分母の項の最小次数
分母の項の最小次数![]() .よって分子の方が速く0に近づく.そこで,
.よって分子の方が速く0に近づく.そこで,
![]() とおくと
とおくと
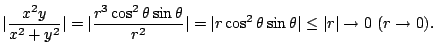
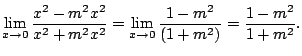
(c)
![]() が
が![]() に近づくとき,
に近づくとき,![]() が0に近づく速さは,
が0に近づく速さは,
![]() が無限大に近づく速さよりも速い.そこで,
が無限大に近づく速さよりも速い.そこで,
![]() とおくと
とおくと