Next: 初等関数(elementary functions) Up: 関数(FUNCTIONS) Previous: 関数の定義(definition of function)
1.1
1.
2.
(a) 定義域は関数f(x)の値が実数をとるような![]() の集合のことである. よって
の集合のことである. よって
![]()
(b) 定義域は関数f(x)の値が実数をとるような![]() の集合のことである.
の集合のことである.
![$ \displaystyle{D(h) = (-\infty,-\frac{1}{2}) \cup (0, \frac{4}{3}]}$](img33.gif)
3.
(b) ![]() が意味を持つには
が意味を持つには![]() の値域が
の値域が![]() の定義域に含まれていなければならない.そこで,
の定義域に含まれていなければならない.そこで,![]() の値域を調べる.
の値域を調べる.
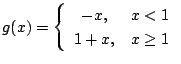
![]() ならば,
ならば,![]() .また,
.また,
![]() ならば,
ならば,
![]() .よって
.よって
![]() のとき,
のとき,
![]() を用い,
を用い,
![]() のとき,
のとき,
![]() を用いる.よって
を用いる.よって
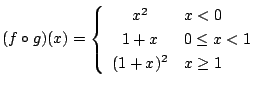
同様に,
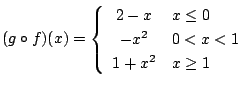
4.
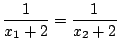 |
|||
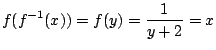
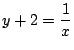 .よって
.よって
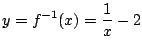 となる.
となる.
(b) この関数は1対1の関数ではない.なぜならば,
![]() より,
より,![]() 軸対称.よって,逆関数は存在しない.ただ,
軸対称.よって,逆関数は存在しない.ただ,![]() が1対1の関数となるように定義域を
が1対1の関数となるように定義域を
![]() と表わすと,これらの定義域において,
と表わすと,これらの定義域において,