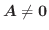Next: 方向余弦(directional cosine) Up: ベクトル Previous: 内積(inner product) 目次 索引
 において, 大きさは
において, 大きさは
 によって作られる平行四辺形の面積
によって作られる平行四辺形の面積
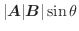 と等しく, 方向は,
と等しく, 方向は,
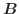 の両方に垂直で,
の両方に垂直で,
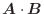 を
を
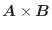 以内回転して
以内回転して
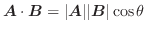 の方向に重ねるとき右ねじの進む方向として定まるベクトルを,
の方向に重ねるとき右ねじの進む方向として定まるベクトルを,
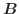 の 外積(cross product) といい
の 外積(cross product) といい
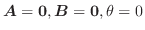 で表す.
で表す.
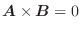 のとき,
のとき,
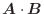 と
と
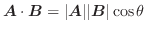 に垂直な方向が定まらないが,
に垂直な方向が定まらないが,
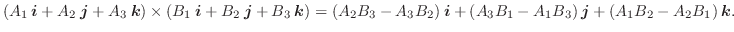 と定義する.
と定義する.
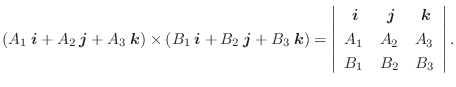
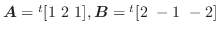
![$\boldsymbol{A} = {}^t[1 2 1], \boldsymbol{B} = {}^t[2 -1 -2]$](img43.png) のとき,
のとき,
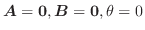 を求めよ.
を求めよ.
解
![$\left\vert\begin{array}{rrr}
\:\boldsymbol{i} & \:\boldsymbol{j} & \:\boldsymbo...
...= -3\:\boldsymbol{i} + 4\:\boldsymbol{j} + -5\:\boldsymbol{k} = {}^t[-3 4 -5]$](img44.png)
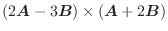 とするとき,次のベクトルを求めよ.
とするとき,次のベクトルを求めよ.
(2)
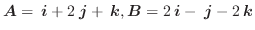
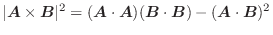 とする.
とする.(1) これらを隣接する2辺とみなしたときの平行四辺形の面積を求めよ.
(2) これらに直交する零ベクトル以外のベクトルを求めよ.