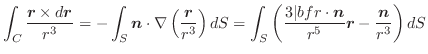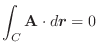Next: 演習問題解答 Up: 積分公式 Previous: ガウスの発散定理(Gauss's divergence theorem) 目次 索引
Stokesの定理
Greenの定理を アイルランドの数学者で物理学者の George Gabriel Stokes (1819-1903) が一般化したものをStokesの定理とよびます.まず, Stokesの定理を学ぶには,曲面の向きづけを行なう必要があります.
|
向きづけられた曲面 ![]() の境界の曲線
の境界の曲線
![]() に沿っての線積分を,
に沿っての線積分を, ![]() 上での面積分に書き換える等式を与えるのがStokesの定理です.
上での面積分に書き換える等式を与えるのがStokesの定理です.
|
証明
まず,
![$\iint_{S} [\nabla \times F_{1}\boldsymbol{i}] \cdot\boldsymbol{n}dS$](img513.png) を考えよう.
を考えよう.
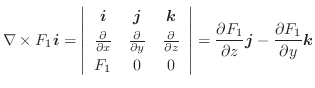
![$\boldsymbol{r} = {}^t[x,y,z]$](img516.png) を位置ベクトルとすると,
を位置ベクトルとすると,
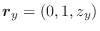 は
は 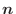 とは直交する.よって
とは直交する.よって
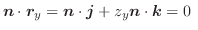 または
または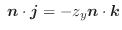
![$\displaystyle [\nabla \times F_{1}\boldsymbol{i}] \cdot\boldsymbol{n}dS = - \le...
...ac{\partial F_{1}}{\partial y} \right ) \boldsymbol{n} \cdot \boldsymbol{k} dS $](img520.png)
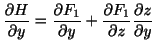
![$\displaystyle [\nabla \times F_{1}\boldsymbol{i}] \cdot\boldsymbol{n}dS = - \fr...
...}\boldsymbol{n} \cdot \boldsymbol{k} dS = - \frac{\partial H}{\partial y}dx dy $](img521.png)
![$\displaystyle \iint_{S}[\nabla \times F_{1}\boldsymbol{i}] \cdot\boldsymbol{n}dS = \iint_{\Omega}- \frac{\partial H}{\partial y}dx dy $](img522.png)
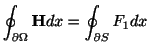
![$\displaystyle \iint_{S}[\nabla \times F_{1}\boldsymbol{i}] \cdot\boldsymbol{n}dS = \oint_{\partial S}{F_{1}}dx $](img523.png)
![$\displaystyle \iint_{S}[\nabla \times F_{2}\boldsymbol{j}] \cdot\boldsymbol{n}d...
...times F_{3}\boldsymbol{k}] \cdot\boldsymbol{n}dS = \oint_{\partial S}{F_{3}}dz $](img524.png)
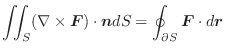
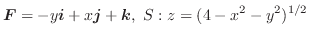 のとき,Stokesの定理が成り立つことを示してみましょう.
のとき,Stokesの定理が成り立つことを示してみましょう.
解
![]() の境界
の境界
![]() は
は
![]() の円となります.よって位置ベクトル
の円となります.よって位置ベクトル
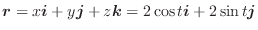 より線積分を求めると
より線積分を求めると
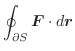 |
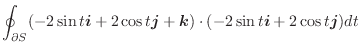 |
||
![$\displaystyle \int_{0}^{2\pi}[4\sin^{2}{t} + 4\cos^{2}{t}]dt = 8\pi$](img1076.gif) |
次に面積分を求めてみます.

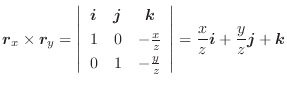
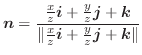
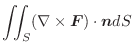 |
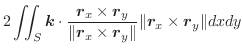 |
||
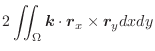 |
|||
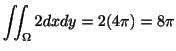 |
これまでに保存場では,ベクトル場はスカラー場の勾配と等しくなり,またベクトル場の回転は0になることをすでに学びました.では線積分との関係においては,どんなことが成り立つのか調べてみましょう.
|
証明
(1)
![]() (2)
(2)
![]() (3)
(3)
![]() (1)を示す.
(1)を示す.
(1)
![]() (2)
(2)
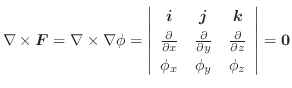
(2)
![]() (3) 閉曲線
(3) 閉曲線 ![]() で囲まれた曲面
で囲まれた曲面 ![]() を考えて,Stokesの定理を使うと
を考えて,Stokesの定理を使うと
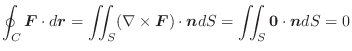
(3)
![]() (1) 定点P
(1) 定点P
![]() と動点Q
と動点Q![]() をむすぶ2つの曲線
をむすぶ2つの曲線
![]() をとり,Pから
をとり,Pから ![]() を経てQに至り,Qから
を経てQに至り,Qから ![]() を逆向きに通ってPに戻る道を
を逆向きに通ってPに戻る道を ![]() とすると,
とすると,
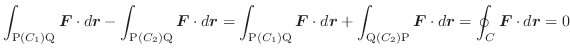
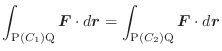
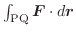 は途中の経路に関係なく,終点Qの座標
は途中の経路に関係なく,終点Qの座標
|
PからQに至る任意の曲線のベクトル方程式を
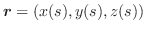 とすると,
とすると,
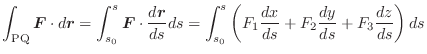
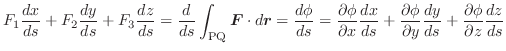
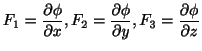
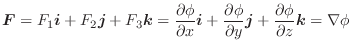
この定理より,線積分をおこなうときに,ベクトル場がスカラー・ポテンシャルを持てば,積分をしなくとも答は0であることが分かります.
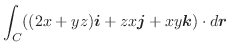 を求めてみましょう.ただし,
を求めてみましょう.ただし, 解
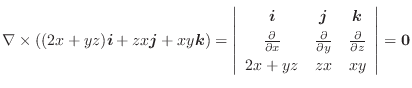
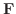 はスカラーポテンシャルを持つ.そこで,
はスカラーポテンシャルを持つ.そこで,
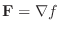 となる
となる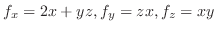 より,
より,
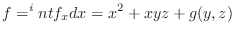
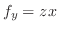 を用いると
を用いると
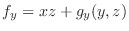 . よって,
. よって,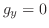 . つまり,
. つまり,
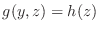 . つぎに,
. つぎに,
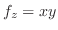 を用いると
を用いると
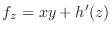 . よって
. よって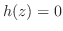 .ここで,
.ここで,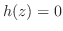 とおくと,
とおくと,
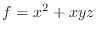
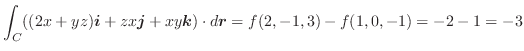
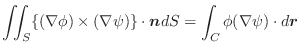
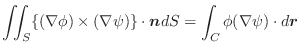
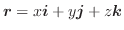 とする.任意の曲面
とする.任意の曲面
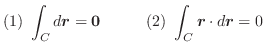
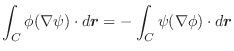
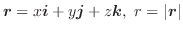 とし,
とし,
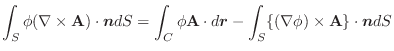
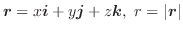 とし,
とし,