度数分布表(Frequency Tabulations)

サンプリング

データの収集過程やサイコロを投げるなどの試行を繰り返すことにより結果を得る過程をサンプリング(sampling)といいます．サンプリングの結果えられたものをサンプル(sample)または標本といいます．

例えば，次のようなデータを得たとしましょう．

例題 1..1  

表: がん患者のヘモグロビン濃度

13.6	14.8	13.7	14.2	11.5
11.9	13.8	14.6	14.2	12.7
13.4	11.5	11.9	14.8	12.7
12.4	15.3	15.2	13.5	15.0
12.4	12.0	13.8	11.7	10.0
13.2	15.5	14.0	13.5	15.0
12.7	12.9	13.7	15.1	13.5
15.7	12.7	15.7	10.9	14.0
14.8	14.0	13.8	12.7	11.9
12.0	11.4	11.1	13.7	13.2

このデータを見ただけでは，どんな結果がでたのか分かりにくいので，これらのデータを整理して分かりやすい表にすることを考えます．データの整理の方法として度数分布表(frequency table)を用いることがよくありますので，度数分布表の作り方を学びます．

データの値を$x_{i}$で表すとき，$x_{i}$が現れる回数を度数(frequency)といい，$f_{i}$で表すと，

$$f_{1}+f_{2}+\cdots+f_{k} = n$$

ただし，$n$はデータの数です．これより，度数を表にしたものを作成することができます．

可能な値	度数
$x_{1}$	$f_{1}$
$x_{2}$	$f_{2}$
$\vdots$	$\vdots$
$x_{k}$	$f_{k}$
合計	n

しかし，データの多くは小数点以下を切り捨てたり，四捨五入したりして得たものなので，$x_{i}$という値で表を作成する代わりに，$a$以上$b$未満での度数という形で表を作成します．このとき，データを$a$以上$b$未満というようないくつかの区間に分けて集計するときの各区間を階級(class interval)といい，$a \sim b$で表します．そして， 区間の幅つまり$b-a$を階級幅(class interval width)といいます．それぞれの区間の端点の相加平均 $${\frac{a + b}{2}}$$を階級値(midpoint)といいます．また，全標本の個数$n$に対する各階級の度数の割合$f_{i}/n$を相対度数(relative frequency)いいます． さらに，統計解析のために$f_{i}$以下の度数の合計

$$F_{i}=f_{1}+f_{2}+\cdots+f_{i}$$

を考えます．これを累積度数といいます．これらを用いて表したものが度数分布表(frequency distribution)です． では，上記のデータを用いて度数分布表を作成してみましょう．データの値が10.0〜15.7なので，階級幅を0.9にとると7個の階級を用いることにより全てのデータを含むことが可能です．ただし，データの値が階級の境界値となるのはおかしいので，最初の階級を9.95から始めます．

表: 度数分布表

階級	階級値	度数	相対度数	累積度数	累積相対度数
9.95 $\sim$ 10.85	10.4	1	0.02	1	0.02
10.85 $\sim$ 11.75	11.3	6	0.12	7	0.14
11.75 $\sim$ 12.65	12.2	7	0.14	14	0.28
12.65 $\sim$ 13.55	13.1	12	0.24	26	0.52
13.55 $\sim$ 14.45	14.0	12	0.24	38	0.76
14.45 $\sim$ 15.35	14.9	9	0.18	47	0.94
15.35 $\sim$ 16.25	15.8	3	0.06	50	1.00

度数分布表を図（棒グラフ）で表したものをヒストグラム(histogram) といいます．また，変量の小さい階級から順に度数を加えていったものを累積度数(cumulative distribution function) といいます．

図: ヒストグラム

図: 累積度数分布図

Sturgesの式

データ数$n$に対して階級数を決める一つの目安にスタージスの式があります．

階級数 = $1 + \frac{\log_{10}{n}}{\log_{10}{2}}$

この式を用いて例題(1.1)の階級数を求めてみると，標本数$n$が50より，階級数$k$は

$$k = 1 + \frac{\log_{10}{50}}{\log_{10}{2}} = 1 + 3.32\log_{10}{50} = 1+3.32(1.699) = 6.64 \approx 7$$

となります．また，階級幅は(最大値-最小値)/階級数で求まるので，階級幅は(15.7-10.0)/6.64 = 0.86となります．したがって，階級幅を0.9とすると階級数は7となります．

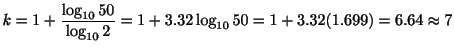
標本の代表値

度数分布表が得られると，データ全体を視覚的に把握することができるようになります．しかしながら，それはあくまで直感的なことです．そこで，直感に頼るのではなく理論的にデータを処理するために，データの特徴を数値で表します．

代表値 : 分布の特徴を代表する数値

変量$x$に関する$n$個のデータ $x_{1},x_{2},\ldots,x_{n}$が与えられたとき，

$$T = x_{1} + x_{2} + \cdots x_{n} = \sum_{i=1}^{n}x_{i}$$

を標本総計値(total)といいます． また，

$$\overline{x} = \frac{x_{1} + x_{2} + \cdots x_{n}}{n} = \frac{1}{n}\sum_{i=1}^{n}x_{i} = \frac{T}{n}$$

を標本平均値(mean)といいます．また変量$x$の値が $x_{1},x_{2},\ldots,x_{k}$で，その度数が $f_{1},f_{2},\ldots,f_{k}$で与えられているとき，標本総計値は

$$T = x_{1}f_{1} + x_{2}f_{2} + \cdots + x_{n}f_{n}$$

となるので，標本平均値は

$$\overline{x} = \frac{x_{1}f_{1} + x_{2}f_{2} + \cdots + x_{n}f_{n}}{n} = \frac{1}{n} \sum_{i=1}^{k}x_{i}f_{i}$$

で与えられます．

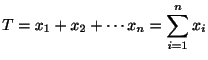
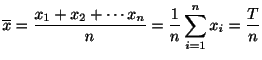
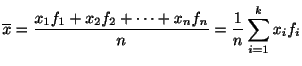
変量の測定値を，大きさの順に並べたとき，中央の位置にくるものを，ミディアン(median)または中央値といいます．データの数$n$が偶数のときは第 $${\frac{n}{2}}$$番目と第 $${\frac{n}{2} + 1}$$番目の変量の平均が中央値．また，データの数$n$が奇数のときは第 $${\frac{n+1}{2}}$$番目の変量が中央値となります．

度数が最も大きい標本値$x_{i}$，または階級値$m_{i}$をモード(mode)または最頻値といいます．

確認問題

• 例題(1.1)の中央値を求めよ．
• 例題( 1.1)のモードを求めよ．

統計学演習問題 1

1. 次のデータについて，スタージェスの式をもちいて度数分布表・ヒストグラム・累積度数分布図を作成しよう．また，平均値，最大値，最小値，中央値，最頻値を求めよう．

コンクリート円柱の引っ張りの強さ$(g/cm^2)$

320	380	340	410	380	340	360	350	320	370
350	340	350	360	370	350	380	370	300	420
370	390	390	440	330	390	330	360	400	370
320	350	360	340	340	350	350	390	380	340
400	360	350	390	400	350	360	340	370	420
420	400	350	370	330	320	390	380	400	370
390	330	360	380	350	330	360	300	360	360
360	390	350	370	370	350	390	370	370	340
370	400	360	350	380	380	360	340	330	370
340	360	390	400	370	410	360	400	340	360