Next: 適合度検定 Up: 統計的検定 Previous: 母集団が正規分布で2標本の場合 目次 索引
母比率の検定(大標本の場合)
母集団の中で,ある属性に対して事象![]() の起こる割合
の起こる割合![]() を事象
を事象![]() の母比率といいます.この母比率に関する仮説を,標本値から検定することを考えます.
の母比率といいます.この母比率に関する仮説を,標本値から検定することを考えます.
母比率が![]() の二項母集団から抽出された大きさ
の二項母集団から抽出された大きさ![]() の標本を
の標本を
![]() とします.ここで,
とします.ここで,
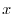
![]() : 「
: 「![]() 」,対立仮説
」,対立仮説 ![]() : 「
: 「
![]() 」
」
を検定することが問題となります.
母比率![]() の二項母集団から大きさ
の二項母集団から大きさ![]() の標本
の標本
![]() をとり,
をとり,
![]() とすると
とすると![]() は二項分布
は二項分布![]() に従います.ここで
に従います.ここで![]() が十分大きいときにはラプラスの定理によって,
が十分大きいときにはラプラスの定理によって,![]() は近似的に正規分布
は近似的に正規分布
![]() に従い,標本比率
に従い,標本比率
![]() は近似的に正規分布
は近似的に正規分布
![]() に従います.よって,標準化を行うと
に従います.よって,標準化を行うと
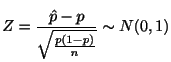
サイコロを600回投げたところ,1の目が108回出たという.1の目が出る母比率![]() は
は
![]() か有意水準5%で検定せよ.
か有意水準5%で検定せよ.
解答
1
![]() : 「1の目の出る確率
: 「1の目の出る確率
![]() 」
」
![]() : 「
: 「
![]() 」
」
2 有意水準
![]()
3 統計量
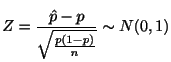
4 ![]() のもとで,
のもとで,
![]() より,
より,
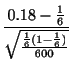 |
|||
5 対立仮説より,標準正規分布の両側確率を用いる.
母比率の差の検定
2つの母集団![]() の中で1つの特性
の中で1つの特性![]() を持つものの母比率を
を持つものの母比率を
![]() とする.この母集団からそれぞれ大きさ
とする.この母集団からそれぞれ大きさ
![]() 個の標本を抽出し,その特性を持つものの個数を
個の標本を抽出し,その特性を持つものの個数を
![]() とする.このとき,母比率について
とする.このとき,母比率について
帰無仮説 ![]() : 「
: 「
![]() 」と対立仮説
」と対立仮説 ![]() : 「
: 「
![]() 」
」
を検定することを考えます.帰無仮説のもとで,母比率の値
![]() は未知ですが,
は未知ですが,
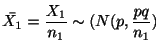
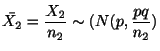
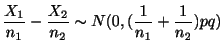
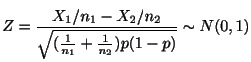
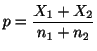
テレビの視聴率調査で,ある番組について男性は400人中の無作為標本中120人が,女性は500人の無作為標本中180人が好きと答えた.実際に男女の好みに差があるといえるか,有意水準5%で検定せよ.
解答 ある番組を男性が好きな比率を![]() ,女性が好きな比率を
,女性が好きな比率を![]() とすると,
とすると,
![]()
1
![]() : 「男女で好みに差がない」
: 「男女で好みに差がない」
![]()
![]() : 「男女で好みに差がある」
: 「男女で好みに差がある」
![]()
2 有意水準
![]()
3 統計量
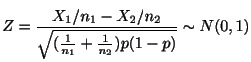
4 ![]() のもとで,
のもとで,
![]() より,
より,
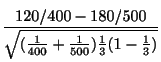 |
|||
5 対立仮説より,標準正規分布の両側確率を用いる.
|
1 ある政党の支持率は従来28%であったが,最近の世論調査で無作為に抽出された3,000人有権者のうち支持率は25%であった.支持率が低下したと判断すべきか,有意水準5%で検定せよ.
2 あるテレビ番組の視聴率調査を男女別に行った.その結果,男性の無作為標本200人のうち25人が,女性の無作為標本300人のうち20人が見ていると答えた.このとき,男女の視聴率に差があるといえるか,有意水準5%で検定せよ.