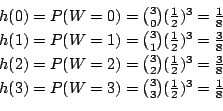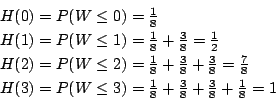2次元確率分布

数理統計演習問題 5

1. 2個のサイコロの出る目の確率変数をとするとき，積の確率分布と分布関数を求めよ．

2. 一枚の銅貨を投げて表が出れば1，裏が出れば0と表すことにする．3枚の銅貨を投げるとき，それぞれの銅貨の表が出ることの確率変数をとする．

(a): 和の確率分布を求めよ．
(b): 和の分布関数を求めよ．

問題解答

(1) とおくとの変域は $\{1,2,3,4,5,6,8,9,10,12,15,16,18,20,24,25,30,36\}$ である．また，確率分布はで与えれることに注意する．まず，を考えてみよう．より，2個のサイコロを投げて両方1の目が出る確率を求めることと同じである．場合の数を求めると，両方1の目の組み合わせは36通り中の1通り．したがって $P(W = 1) = \frac{1}{36}$ ．同様に， $W = 2,3,4,\ldots,36$ について求めると

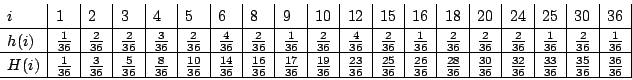
$\begin{displaymath}\begin{array}{l\vert l\vert l\vert l\vert l\vert l\vert l\ver... ...ac{33}{36}&\frac{35}{36}&\frac{36}{36} \hline \par\end{array}\end{displaymath}$

(2) a とおくとの変域は $\{0,1,2,3\}$ である．確率分布はで与えれれる．まず，を考えてみよう．より，3枚銅貨を投げて全て裏が出る確率を求めることと同じである．場合の数を求めると，全部裏の組み合わせは8通り中の1通り．したがって $P(W = 0) = \frac{1}{8}$ ．同様に，について求めると

$\begin{displaymath}\begin{array}{l} h(0) = P(W = 0) = {3 \choose 0}(\frac{1}{2})... ...) = {3 \choose 3}(\frac{1}{2})^{3} = \frac{1}{8}\\ \end{array}\end{displaymath}$

となる． b 分布関数

を求める． $H(i) = P(W \leq i)$ のことなので，

$\begin{displaymath}\begin{array}{l} H(0) = P(W \leq 0) = \frac{1}{8}\\ H(1) = P... ...8} + \frac{3}{8} + \frac{3}{8} + \frac{1}{8} = 1\\ \end{array}\end{displaymath}$