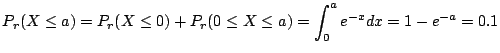Next: 2次元確率分布 Up: 確率変数 Previous: 確率変数 目次
(1) 男児と女児の出生率が等しいと仮定して,4児を持つ家庭の確率変数![]() の値と確率分布
の値と確率分布![]() を求めよ.
を求めよ.
(2) 1つの袋に赤玉4個と白玉6個が入っている.同時に3個の球を取り出す場合,赤玉の個数を表わす確率変数![]() と確率分布
と確率分布![]() を求め,そのグラフをかこう.また,
を求め,そのグラフをかこう.また,
![]() を求めよう.
を求めよう.
3. 与えられた
![]() に対して,関数
に対して,関数
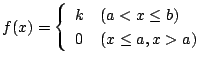
が与えられている.
4. 確率密度が
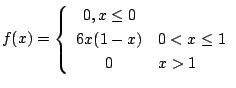
で与えられている.
5. 関数
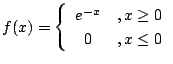
が与えられている.
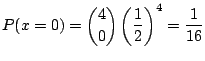
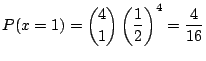
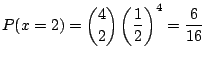
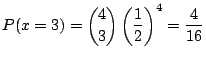
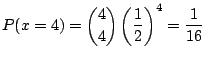
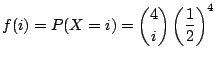
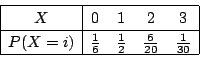
2. 10個から3個取り出す組み合わせは
![]() 通り.また,3個中赤がゼロということは,白が3個と同じことなので,6個の白から3個取り出すこととなり,その組み合わせは
通り.また,3個中赤がゼロということは,白が3個と同じことなので,6個の白から3個取り出すこととなり,その組み合わせは
![]() 通り.よって,
通り.よって,![]() を赤玉の個数とおくと,
を赤玉の個数とおくと,
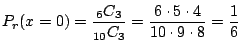
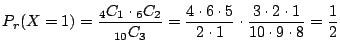
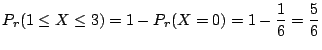
3.
を満たしていることを示せばよい. そこで,
1. 定数![]() を0以上とすれば
を0以上とすれば
![]() は満たされる.
は満たされる.
2.
![]() より
より
![]() と定めればよい.
と定めればよい.
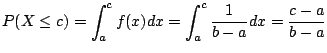
(4)
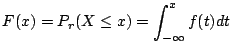
![]() のとき
のとき
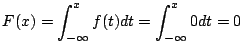
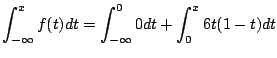 |
|||
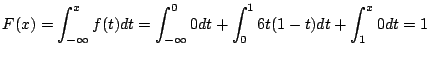
4.
![]() と
と
![]() を示せばよいでしょう.
を示せばよいでしょう.
1.
![]() は指数関数より全ての
は指数関数より全ての![]() で
で![]() .
.
2.
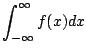 |
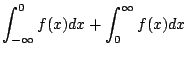 |
||
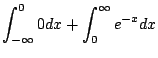 |
|||