next up previous contents
Next: 多次元確率分布 Up: 確率変数 Previous: 2次元確率分布   目次

確率変数の平均値と分散

数理統計演習問題 6

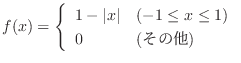
1. $f(x) = \left\{\begin{array}{ll} 1 - \vert x\vert & (-1 \leq x \leq 1)\\ 0 & (\mbox{その他}) \end{array}\right. $
のとき次の問いに答えよう．

(a)
$ f(x)$は確率密度関数であることを示そう．
(b)
分布関数$ F(x)$を求めよう．
(c)
$ P_{r}(-\frac{1}{2} \leq X \leq \frac{1}{2})$を求めよう．
(d)
$ E(X), V(X)$を求めよう．

2. 1つのサイコロを，3回投げるとき，1の目が出る回数を$ X$とする．

(a)
$ X$の確率分布を求めよう．
(b)
$ X$の平均と標準偏差を求めよう．
(c)
$ X$を標準化した確率変数$ Z$を求め，更に，$ Z$の確率分布を求めよう．

3. Bernoulliの定理を利用して，次の確率を求めよう．

(a)
1枚の硬貨を1000回投げたとき，表が現われる回数$ r$が

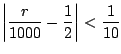
$\displaystyle \left\vert\frac{r}{1000} - \frac{1}{2}\right\vert < \frac{1}{10} $

を満たす確率．
(b)
2枚の硬貨を1000回投げたとき，2枚とも表が現われる回数$ r$が，

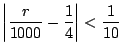
$\displaystyle \left\vert\frac{r}{1000} - \frac{1}{4}\right\vert < \frac{1}{10} $

をみたす確率．
(c)
1枚の硬貨を2000回投げて，表の出る回数が1000回より50回以内の偏りである確率を求めよ．
(d)
1枚の硬貨を2000回投げて，表の出る割合と理論的確率$ 0.5$との差が$ 5\%$以内である確率が$ 99\%$以上であるようにするには，何回以上投げればよいか．

問題解答

(1)

a

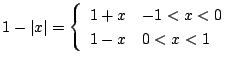
$\displaystyle 1 - \vert x\vert = \left\{\begin{array}{cl} 1 + x & -1 < x < 0\\ 1 - x & 0 < x < 1 \end{array}\right. $

より $ f(x) \geq 0$．また
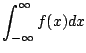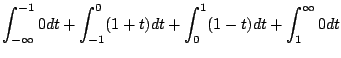$\displaystyle \int_{-\infty}^{\infty} f(x) dx$ $\displaystyle =$ $\displaystyle \int_{-\infty}^{-1} 0dt + \int_{-1}^{0} (1 + t)dt + \int_{0}^{1} (1-t)dt + \int_{1}^{\infty} 0 dt$  
  $\displaystyle =$ $\displaystyle \left[t + \frac{t^2}{2}\right]_{-1}^{0} + \left[t - \frac{t^2}{2}\right]_{0}^{1}$  
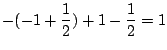  $\displaystyle =$ $\displaystyle -(-1 + \frac{1}{2}) + 1 - \frac{1}{2} = 1$  

別解 $ f(x) \geq 0$より， $ \int_{-\infty}^{\infty} f(x) dx$は$ f(x)$と$ x$軸の間の面積と考えられる．したがって，求める面積は底辺2高さ1の三角形の面積より1．

b

$ x < -1$のとき

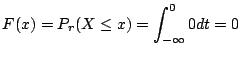
$\displaystyle F(x) = P_{r}(X \leq x) = \int_{-\infty}^{0} 0dt = 0 $

$ -1 < x < 0$のとき
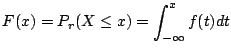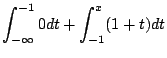$\displaystyle F(x) = P_{r}(X \leq x) = \int_{-\infty}^{x} f(t) dt $ $\displaystyle =$ $\displaystyle \int_{-\infty}^{-1} 0dt + \int_{-1}^{x} (1 + t)dt$  
  $\displaystyle =$ $\displaystyle \left[t + \frac{t^2}{2}\right]_{-1}^{x}$  
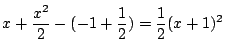  $\displaystyle =$ $\displaystyle x + \frac{x^2}{2} -(-1 + \frac{1}{2}) = \frac{1}{2}(x+1)^2$  

$ 0 < x < 1$のとき，
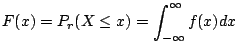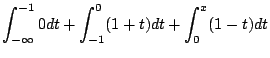$\displaystyle F(x) = P_{r}(X \leq x) = \int_{-\infty}^{\infty} f(x) dx$ $\displaystyle =$ $\displaystyle \int_{-\infty}^{-1} 0dt + \int_{-1}^{0} (1 + t)dt + \int_{0}^{x} (1-t)dt$  
  $\displaystyle =$ $\displaystyle \left[t + \frac{t^2}{2}\right]_{-1}^{0} + \left[t - \frac{t^2}{2}\right]_{0}^{x}$  
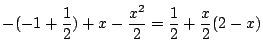  $\displaystyle =$ $\displaystyle -(-1 + \frac{1}{2}) + x - \frac{x^2}{2} = \frac{1}{2} + \frac{x}{2}(2 - x)$  

c

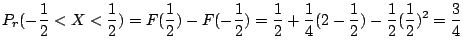
$\displaystyle P_{r}(-\frac{1}{2} < X < \frac{1}{2}) = F(\frac{1}{2}) - F(-\frac... ...}{2} + \frac{1}{4}(2 - \frac{1}{2}) - \frac{1}{2}(\frac{1}{2})^2 = \frac{3}{4} $

d

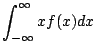$\displaystyle E(X)$ $\displaystyle =$ $\displaystyle \int_{-\infty}^{\infty} x f(x) dx$  
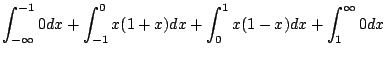  $\displaystyle =$ $\displaystyle \int_{-\infty}^{-1} 0dx + \int_{-1}^{0}x(1+x)dx + \int_{0}^{1}x(1-x)dx + \int_{1}^{\infty} 0dx$  
  $\displaystyle =$ $\displaystyle \left[\frac{x^2}{2} + \frac{x^3}{3}\right]_{-1}^{0} + \left[\frac{x^2}{2} - \frac{x^3}{3}\right]_{0}^{1} = 0$  


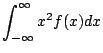$\displaystyle E(X^2)$ $\displaystyle =$ $\displaystyle \int_{-\infty}^{\infty} x^2 f(x) dx$  
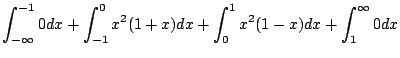  $\displaystyle =$ $\displaystyle \int_{-\infty}^{-1} 0dx + \int_{-1}^{0}x^2(1+x)dx + \int_{0}^{1}x^2(1-x)dx + \int_{1}^{\infty} 0dx$  
  $\displaystyle =$ $\displaystyle \left[\frac{x^3}{3} + \frac{x^4}{4}\right]_{-1}^{0} + \left[\frac{x^3}{3} - \frac{x^4}{4}\right]_{0}^{1}$  
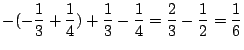  $\displaystyle =$ $\displaystyle -(-\frac{1}{3} + \frac{1}{4}) + \frac{1}{3} - \frac{1}{4} = \frac{2}{3} - \frac{1}{2} = \frac{1}{6}$  

これより

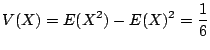
$\displaystyle V(X) = E(X^2) - E(X)^2 = \frac{1}{6} $

2.

a 1の目が出る回数を$ X$とすると，

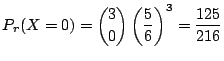
$\displaystyle P_{r}(X = 0) = \binom{3}{0}\left(\frac{5}{6}\right)^3 = \frac{125}{216}$

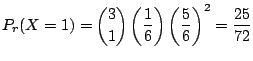
$\displaystyle P_{r}(X = 1) = \binom{3}{1}\left(\frac{1}{6}\right)\left(\frac{5}{6}\right)^{2} = \frac{25}{72} $

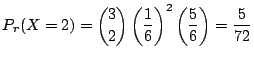
$\displaystyle P_{r}(X = 2) = \binom{3}{2}\left(\frac{1}{6}\right)^2 \left(\frac{5}{6}\right) = \frac{5}{72} $

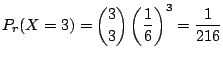
$\displaystyle P_{r}(X = 3) = \binom{3}{3}\left(\frac{1}{6}\right)^3 = \frac{1}{216} $

別解 この試行はベルヌーイ試行である．つまり，

事象「1の目がでる」が発生するか否かを問う
この事象の発生はそれぞれの試行において独立である
この事象の発生は各試行において一定である

ベルヌーイ試行を$ n$回行なったとき，事象の発生回数$ X$を$ i$，事象の発生確率を$ p$とすると

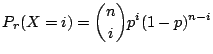
$\displaystyle P_{r}(X = i) = \binom{n}{i}p^{i}(1-p)^{n-i} $

となり，$ X$は2項分布に従うといい， $ X \sim B(n,p)$と表わします．このとき，

$\displaystyle E(X) = np, V(X) = np(1-p) $

が知られています．

b

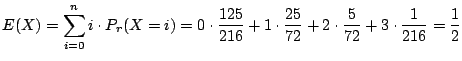
$\displaystyle E(X) = \sum_{i=0}^{n} i \cdot P_{r}(X = i) = 0\cdot \frac{125}{21... ...dot \frac{25}{72} + 2 \cdot \frac{5}{72} + 3 \cdot \frac{1}{216} = \frac{1}{2} $

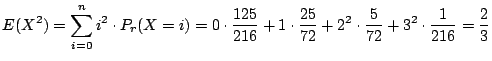
$\displaystyle E(X^2) = \sum_{i=0}^{n} i^2 \cdot P_{r}(X = i) = 0\cdot \frac{125... ...\frac{25}{72} + 2^2 \cdot \frac{5}{72} + 3^2 \cdot \frac{1}{216} = \frac{2}{3} $

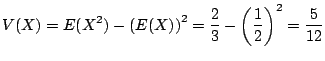
$\displaystyle V(X) = E(X^2) - \left(E(X)\right)^2 = \frac{2}{3} - \left(\frac{1}{2}\right)^2 = \frac{5}{12} $

したがって，

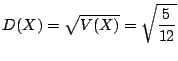
$\displaystyle D(X) = \sqrt{V(X)} = \sqrt{\frac{5}{12}} $

別解

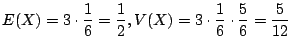
$\displaystyle E(X) = 3\cdot \frac{1}{6} = \frac{1}{2}, V(X) = 3\cdot\frac{1}{6}\cdot \frac{5}{6} = \frac{5}{12} $

c $ X$の標準化とは平均$ \mu$を0に分散$ \sigma^2$を1に変えることである．そこで$ X$の標準化は

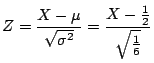
$\displaystyle Z = \frac{X - \mu}{\sqrt{\sigma^2}} = \frac{X - \frac{1}{2}}{\sqrt{\frac{1}{6}}} $

次に$ Z$の確率分布を求めてみよう．

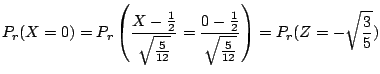
$\displaystyle P_{r}(X = 0) = P_{r}\left(\frac{X - \frac{1}{2}}{\sqrt{\frac{5}{1... ...0 - \frac{1}{2}}{\sqrt{\frac{5}{12}}}\right) = P_{r}(Z = - \sqrt{\frac{3}{5}}) $

より

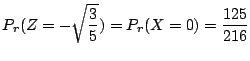
$\displaystyle P_{r}(Z = - \sqrt{\frac{3}{5}}) = P_{r}(X = 0) = \frac{125}{216} $

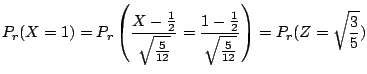
$\displaystyle P_{r}(X = 1) = P_{r}\left(\frac{X - \frac{1}{2}}{\sqrt{\frac{5}{1... ...c{1 - \frac{1}{2}}{\sqrt{\frac{5}{12}}}\right) = P_{r}(Z = \sqrt{\frac{3}{5}}) $

より

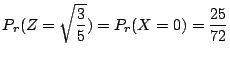
$\displaystyle P_{r}(Z = \sqrt{\frac{3}{5}}) = P_{r}(X = 0) = \frac{25}{72} $

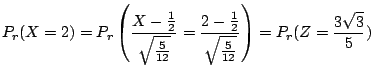
$\displaystyle P_{r}(X = 2) = P_{r}\left(\frac{X - \frac{1}{2}}{\sqrt{\frac{5}{1... ...{2 - \frac{1}{2}}{\sqrt{\frac{5}{12}}}\right) = P_{r}(Z = \frac{3\sqrt{3}}{5}) $

より

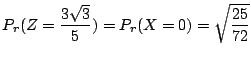
$\displaystyle P_{r}(Z = \frac{3\sqrt{3}}{5}) = P_{r}(X = 0) = \sqrt{\frac{25}{72}} $

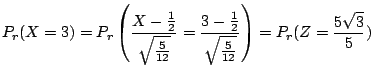
$\displaystyle P_{r}(X = 3) = P_{r}\left(\frac{X - \frac{1}{2}}{\sqrt{\frac{5}{1... ...{3 - \frac{1}{2}}{\sqrt{\frac{5}{12}}}\right) = P_{r}(Z = \frac{5\sqrt{3}}{5}) $

より

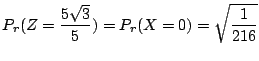
$\displaystyle P_{r}(Z = \frac{5\sqrt{3}}{5}) = P_{r}(X = 0) = \sqrt{\frac{1}{216}} $

3

a Bernoulliの定理は試行回数が$ n$，事象発生回数が$ r$，事象発生確率が$ p$のとき

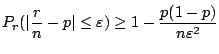
$\displaystyle P_{r}(\vert\frac{r}{n} - p\vert \leq \varepsilon) \geq 1 - \frac{p(1-p)}{n \varepsilon^2} $

が成り立つといっているので，

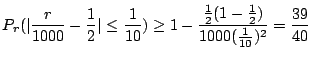
$\displaystyle P_{r}(\vert\frac{r}{1000} - \frac{1}{2}\vert \leq \frac{1}{10}) \geq 1 - \frac{\frac{1}{2}(1-\frac{1}{2})}{1000 (\frac{1}{10})^2} = \frac{39}{40}$

b

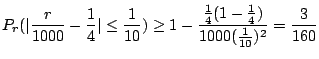
$\displaystyle P_{r}(\vert\frac{r}{1000} - \frac{1}{4}\vert \leq \frac{1}{10}) \geq 1 - \frac{\frac{1}{4}(1-\frac{1}{4})}{1000 (\frac{1}{10})^2} = \frac{3}{160}$

c この問題は試行回数が2000のとき，事象発生回数$ r$の偏りが50回以内である確率を求めよということである．言い換えると，2000回中の表が現われる割合 $ \frac{r}{2000}$と理論的確率 $ p = \frac{1}{2}$との誤差が $ \frac{50}{1000}$である確率を求めよということになる．そこでBernoulliの定理を用いると

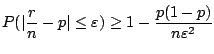
$\displaystyle P(\vert\frac{r}{n} - p\vert \leq \varepsilon) \geq 1 - \frac{p(1-p)}{n \varepsilon^2} $

より
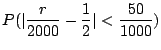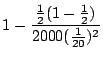$\displaystyle P(\vert\frac{r}{2000} - \frac{1}{2}\vert < \frac{50}{1000})$ $\displaystyle \geq$ $\displaystyle 1 - \frac{\frac{1}{2}(1-\frac{1}{2})}{2000 (\frac{1}{20})^2}$  
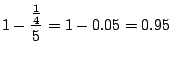  $\displaystyle =$ $\displaystyle 1 - \frac{\frac{1}{4}}{5} = 1 - 0.05 = 0.95$  

d この問題はn回中の表が現われる割合 $ \frac{r}{n}$と理論的確率 $ p = \frac{1}{2}$との誤差が$ 0.05\%$である確率が$ 99\%$以上になるには何回以上投げればよいかということを聞いている．そこでBernoulliの定理を用いると

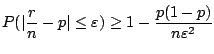
$\displaystyle P(\vert\frac{r}{n} - p\vert \leq \varepsilon) \geq 1 - \frac{p(1-p)}{n \varepsilon^2} $

より $ 1 - \frac{p(1-p)}{n \varepsilon^2} \geq 0.99$である$ n$を求めればよい．
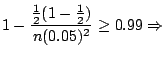$\displaystyle 1 - \frac{\frac{1}{2}(1-\frac{1}{2})}{n (0.05)^2} \geq 0.99 \Rightarrow$      
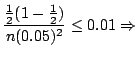$\displaystyle \frac{\frac{1}{2}(1-\frac{1}{2})}{n (0.05)^2} \leq 0.01 \Rightarrow$      
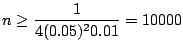$\displaystyle n \geq \frac{1}{4(0.05)^2 0.01} = 10000$      

next up previous contents
Next: 多次元確率分布 Up: 確率変数 Previous: 2次元確率分布   目次