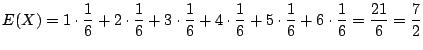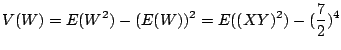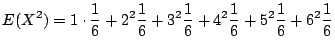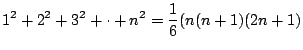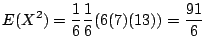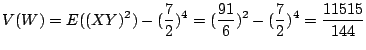Next: 理論分布 Up: 確率変数 Previous: 確率変数の平均値と分散 目次
1. 1枚の銅貨を投げて表が出れば1,裏が出れば0と表わすことにする.3枚の銅貨を投げるとき,それぞれの銅貨の表がでることの確率変数を![]() として,次の問に答えよ.
として,次の問に答えよ.
2. 確率変数![]() の確率密度が次の式
の確率密度が次の式
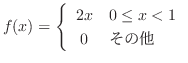
3. 2つのさいころを投げて出た目を確率変数![]() とする.
とする.
1.
a
![]() とおくと
とおくと![]() の変域は
の変域は
![]() である.確率分布
である.確率分布![]() は
は![]() で与えれれる.
まず,
で与えれれる.
まず,![]() を考えてみよう.
を考えてみよう.
![]() より,3枚銅貨を投げて全て裏が出る確率を求めることと同じである.場合の数を求めると,全部裏の組み合わせは8通り中の1通り.したがって
より,3枚銅貨を投げて全て裏が出る確率を求めることと同じである.場合の数を求めると,全部裏の組み合わせは8通り中の1通り.したがって
![]() .同様に,
.同様に,![]() について求めると
について求めると
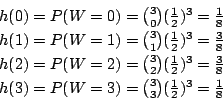
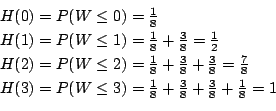
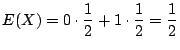
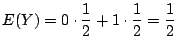
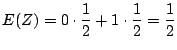
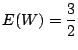
別解 ![]() の確率分布が分かっているので,直接求めることも可能である.
の確率分布が分かっているので,直接求めることも可能である.
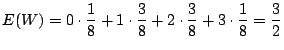
次に![]() の分散
の分散![]() を求める.一般に
を求める.一般に
![]() を用いて求める方が簡単であるが,この問題では
を用いて求める方が簡単であるが,この問題では![]() の確率分布が分かっているので直接求める方が簡単である.
の確率分布が分かっているので直接求める方が簡単である.
![]() より
より
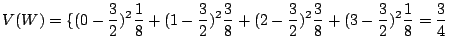
2.
a ![]() の確率密度関数
の確率密度関数![]() を求めるには
を求めるには![]() の分布関数
の分布関数![]() について調べ,
について調べ,
![]() の関係を用いる.
の関係を用いる.
![]() の分布関数
の分布関数![]() は
は
![]() ,
,![]() の分布関数
の分布関数![]() は
は
![]() で与えられるので,
で与えられるので,
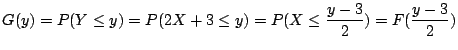
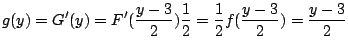
![]() の期待値
の期待値
![]() より
より![]() を求めるには,
を求めるには,![]() を求めればよいことが分かる.
を求めればよいことが分かる.
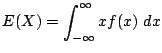 で与えられるので,
で与えられるので,
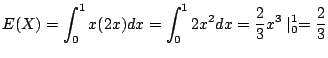
注 : ![]() の確率密度関数を求めたので,直接
の確率密度関数を求めたので,直接![]() を
を
![]() で求めることもできる.
で求めることもできる.
最後に![]() の分散を求める.ここで
の分散を求める.ここで
![]() に注意すると
に注意すると ![]() を求めるには
を求めるには![]() を求めればよいことが分かる.
を求めればよいことが分かる.
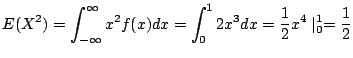
![$\displaystyle V(Y) = V(2X+3) = 4V(X) = 4[E(X^2) - (E(X))^2] = 4[\frac{1}{2} - (\frac{2}{3})^2] = \frac{2}{9}$](img441.gif)
b
![]() の確率密度関数
の確率密度関数![]() を求めるには
を求めるには![]() の分布関数
の分布関数![]() について調べ,
について調べ,
![]() の関係を用いる.
の関係を用いる.
![]() の分布関数
の分布関数![]() は
は
![]() ,
,![]() の分布関数
の分布関数![]() は
は
![]() で与えられるので,
で与えられるので,
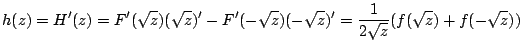
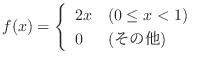
次に期待値を求める.
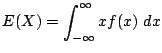 で与えられるので,
で与えられるので,
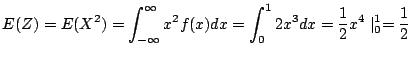
最後に![]() の分散を求める.
の分散を求める.
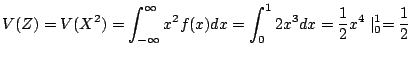
![$\displaystyle V(Y) = V(2X+3) = 4V(X) = 4[E(X^2) - (E(X))^2] = 4[\frac{1}{2} - (\frac{2}{3})^2] = \frac{2}{9}$](img441.gif)
3.