正規分布

数理統計演習問題10

1. $X \sim N(170,10^2)$ のとき，次の確率を求めよう．

(a): $P_{r}(X \leq 160)$
(b): $P_{r}(160 \leq X \leq 175)$

2. $Z \sim N(0,1)$ のとき，次の式を満たす $\lambda$ を求めよ．

(a): $P_{r}(Z > \lambda) = 0.05$
(b): $P_{r}(\vert Z\vert > \lambda) = 0.05$

3. 全国の20才に男子の身長は正規分布に従うものとする．

(a): 身長の大きさに順に総数を10等分するためには，境界値をいくらにすればよいか．
(b): 20才の男子120名を抽出して，身長の平均値が168.9cmより1.3cm以上かたよる確率を求めよ．

4. 2項分布，ポワソン分布，正規分布について，次のことがいえます．
$X \sim B(n,p)$ のとき，

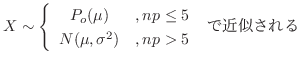
$\displaystyle X \sim \left\{\begin{array}{cl} P_{o}(\mu) &, np \leq 5\\ N(\mu,\sigma^2)&, np > 5 \end{array}\right. \ \mbox{で近似される}$

このことを用いて次の質問に答えよう．

(a): $X \sim B(100,0.02)$ のとき， $P_{r}(X \geq 2)$ を求めよ．
(b): $X \sim B(100, 0.2)$ のとき， $P_{r}(X \geq 25)$ を求めよ．
(c): 1個のさいころを600回投げて，1の目の出る回数が90回以上100回以下である確率を近似せよ．
(d): 100枚の偏りのない硬貨を同時に投げる．表の出る回数が40以上60以下の確率を近似せよ．

問題解答

1. $X \sim N(170,10^2)$ より， $Z = \frac{X - 170}{10}$ とおくと， $Z \sim N(0,1)$ となる。

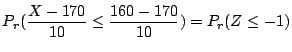$\displaystyle P_{r}(X \leq 160)$	$\displaystyle =$	$\displaystyle P_{r}(\frac{X - 170}{10} \leq \frac{160 - 170}{10}) = P_{r}(Z \leq -1)$
	$\displaystyle =$	$\displaystyle 0.5 - P_{r}(0 \leq Z \leq 1) = 0.5 - 0.3413 = 0.1587$

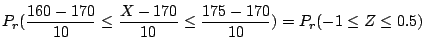$\displaystyle P_{r}(160 \leq X \leq 175)$	$\displaystyle =$	$\displaystyle P_{r}(\frac{160 - 170}{10} \leq \frac{X - 170}{10} \leq \frac{175 - 170}{10}) = P_{r}(-1 \leq Z \leq 0.5)$
	$\displaystyle =$	$\displaystyle P_{r}(-1 \leq Z \leq 0) + P_{r}(0 \leq Z \leq 0.5) = 0.3413 + 0.1915 = 0.5328$

$P_{r}(\vert Z\vert > \lambda) = 0.05$ を満たす $\lambda$ を求める。標準正規分布表により， $P_{r}(0 \leq Z \leq z)$ の値が与えられている。そこで，

$\displaystyle P_{r}(\vert Z\vert > \lambda) = 1 - P_{r}(\vert Z\vert \leq \lambda)$

と書き直すと，

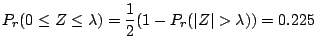
$\displaystyle P_{r}(0 \leq Z \leq \lambda) = \frac{1}{2}(1 - P_{r}(\vert Z\vert > \lambda)) = 0.225$

これより， $\lambda = 1.645$ を得る。

$P_{r}(\vert Z\vert > \lambda) = 0.05$ を満たす $\lambda$ を求める。標準正規分布表により， $P_{r}(0 \leq Z \leq z)$ の値が与えられている。そこで，

$\displaystyle P_{r}(Z > \lambda) = 0.5 - P_{r}(0 \leq Z \leq \lambda)$

と書き直すと，

$\displaystyle P_{r}(0 \leq Z \leq \lambda) = 0.5 - P_{r}(Z > \lambda) = 0.45$

これより， $\lambda = 0.595$ を得る。

平均, 分散 $5.6^{2}$ より正規化すると，

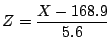
$\displaystyle Z = \frac{X - 168.9}{5.6}$

次に，標準正規分布表より，

$\displaystyle P_{r}(0 \leq Z \leq z) = 0.1, P_{r}(0 \leq Z \leq z) = 0.2, \ldots, P_{r}(0 \leq Z \leq z) = 0.5$

を満たす

を求めると，

$\displaystyle P_{r}(0 \leq Z \leq 0.255)$	$\displaystyle =$	$\displaystyle 0.1$
$\displaystyle P_{r}(0 \leq Z \leq 0.525)$	$\displaystyle =$	$\displaystyle 0.2$
$\displaystyle P_{r}(0 \leq Z \leq 0.845)$	$\displaystyle =$	$\displaystyle 0.3$
$\displaystyle P_{r}(0 \leq Z \leq 1.281)$	$\displaystyle =$	$\displaystyle 0.4$
$\displaystyle P_{r}(0 \leq Z \leq 3.4)$	$\displaystyle =$	$\displaystyle 0.5$

となる。これより，総数を10等分するには，

の値を次のように分ければよい。

$\displaystyle -3.4 \sim -1.281 \sim -0.845 \sim -0.525 \sim -0.255 \sim 0 \sim 0.255 \sim 0.525 \sim 0.845 \sim 1.281 \sim 3.4$

120名の平均身長を $\bar{X}$ とすると，中心極限定理より

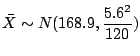
$\displaystyle \bar{X} \sim N(168.9, \frac{5.6^{2}}{120})$

ここで，身長の平均が168.9cmより1.3cm以上かたよる確率は

$\displaystyle P_{r}(\vert\bar{X} - 168.9\vert \geq 1.3) = 1 - 2P_{r}(0 \leq \bar{X} - 168.9 < 1.3)$

で求まる。ここで，

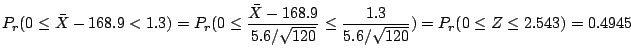
$\displaystyle P_{r}(0 \leq \bar{X} - 168.9 < 1.3) = P_{r}(0 \leq \frac{\bar{X} ... ...rt{120}} \leq \frac{1.3}{5.6/\sqrt{120}}) = P_{r}(0 \leq Z \leq 2.543) = 0.4945$

より，

$\displaystyle P_{r}(\vert\bar{X} - 168.9\vert \geq 1.3) = 1 - 2(0.4945) = 0.011$

$X \sim B(100,0.02)$ より，期待値となり，ポワソン分布で近似できる。 $X \sim P_{o}(\lambda)$ ， $\lambda = E(X) = 2$ より，

$\displaystyle P_{r}(X \geq 2)$	$\displaystyle =$	$\displaystyle 1 - P_{r}(X < 2) = 1 - P_{r}(X = 0) - P_{r}(X = 1)$
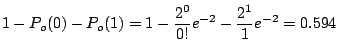	$\displaystyle =$	$\displaystyle 1 - P_{o}(0) - P_{o}(1) = 1 - \frac{2^{0}}{0!}e^{-2} - \frac{2^{1}}{1}e^{-2}= 0.594$

$X \sim B(100, 0.2)$ より，期待値となり，正規分布で近似できる。 $\mu = E(X) = np = 20, \sigma^{2} = V(X) = np(1-p) = 16$ より， $X \sim N(20,4^{2})$ 。これより

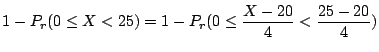$\displaystyle P_{r}(X \geq 25)$	$\displaystyle =$	$\displaystyle 1 - P_{r}(0 \leq X < 25) = 1 - P_{r}(0 \leq \frac{X - 20}{4} < \frac{25-20}{4} )$
	$\displaystyle =$	$\displaystyle 1 - P_{r}(0 \leq Z < 1.25) = 1 - 0.3944 = 0.6056$

を1の目の出る回数とすると， $X \sim B(600,1/6)$ の2項分布に従う。そこで，1の目の出る回数が90回以上100回以下である確率を求めると

$\displaystyle P_{r}(90 \leq X \leq 100) = P_{r}(X = 90) + P_{r}(X = 91) + \cdots + P_{r}(X = 100)$

で求まるが， $\mu = E(X) = np = 100$ , $\sigma^{2} = V(X) = npq = 500/6$ より， $X \sim N(100, 500/6)$ の正規分布で近似できることが分かる。正規分布を用いると

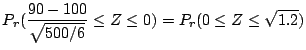$\displaystyle P_{r}(90 \leq X \leq 100)$	$\displaystyle =$	$\displaystyle P_{r}(\frac{90 - 100}{\sqrt{500/6}} \leq Z \leq 0)= P_{r}(0 \leq Z \leq \sqrt{1.2})$
	$\displaystyle =$	$\displaystyle P_{r}(0 \leq Z \leq 1.095) = 0.3621$

を表の目の出る回数とすると， $X \sim B(100, 1/2)$ の2項分布に従う。そこで，表の出る回数が40以上60以下の確率を求めると

$\displaystyle P_{r}(40 \leq X leq 60) = P_{r}(X = 40) + P_{r}(X = 41) + \cdots + P_{r}(X = 60)$

で求まるが， $\mu = E(X) = np = 50$ , $\sigma^{2} = V(X) = npq = 25$ より， $X \sim N(50, 5^{2})$ の正規分布で近似できることが分かる。正規分布を用いると

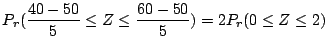$\displaystyle P_{r}(40 \leq X \leq 60)$	$\displaystyle =$	$\displaystyle P_{r}(\frac{40 - 50}{5} \leq Z \leq \frac{60 - 50}{5})= 2P_{r}(0 \leq Z \leq 2)$
	$\displaystyle =$	$\displaystyle 2(.4772) = 0.9544$