Next: 確率変数 Up: 確率モデル Previous: 確率の定義(Definition of probability) 目次
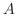 と事象
と事象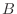 とが同じであるとき,
とが同じであるとき,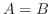 と書く.事象
と書く.事象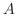 が事象
が事象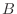 に含まれているとき,
に含まれているとき,
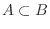 と書く.
と書く.
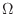 自身で表される事象
自身で表される事象
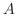 ,
,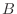 の少なくとも一方が起こる事象.
の少なくとも一方が起こる事象.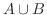 で表す.
で表す.
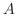 ,
,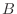 がともに起こる事象.
がともに起こる事象.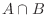 で表す.
で表す.
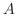 に対して
に対して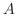 が起こらない事象.
が起こらない事象.
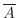 で表す.
で表す.
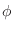 で表す.
で表す.
事象の演算について,集合の場合と同様に次の関係式が成り立つ.
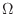 ,空事象を
,空事象を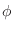 とするとき,
とするとき,
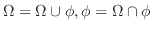
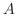 に対して
に対して
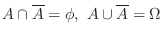
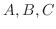 に対して
に対して
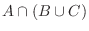 |
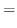 |
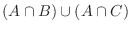 |
|
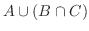 |
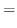 |
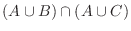 |
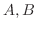 に対して(DeMorganの法則)
に対して(DeMorganの法則)
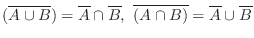
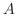 ,
,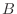 ,
,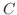 に対して,
に対して,
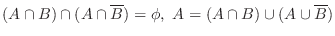
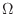 の任意の事象
の任意の事象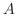 に対して,次の公理を満足する実数
に対して,次の公理を満足する実数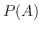 が定まるとき,
が定まるとき,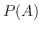 を事象
を事象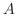 の確率といい,確率が考えられる事象を確率事象という.
の確率といい,確率が考えられる事象を確率事象という.
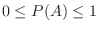
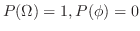
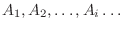 のいずれの2つも互いに排反であれば,
のいずれの2つも互いに排反であれば,
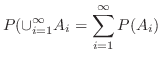
条件確率(conditional probability) 事象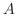 を固定して,事象
を固定して,事象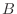 の関数として
の関数として
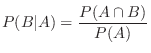
と定義すると,この関数は確率の公理を満たす.これを事象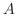 が起こったときの事象
が起こったときの事象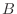 の条件付き確率(conditional probability)という.
の条件付き確率(conditional probability)という.
事象
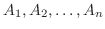 が互いに排反であり,
が互いに排反であり,
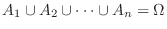
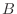 に対して
に対して
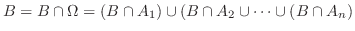
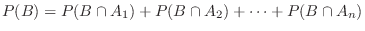
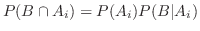 となるので,
となるので,
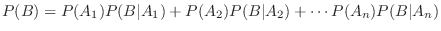
1. 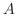 = [さいころを4回投げて少なくとも1回6の目がでる].
= [さいころを4回投げて少なくとも1回6の目がでる]. 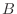 = [2個のさいころを同時に24回投げて少なくとも1回2個とも6の目がでる] とするとき,
= [2個のさいころを同時に24回投げて少なくとも1回2個とも6の目がでる] とするとき,
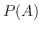 を求めよう.
を求めよう.
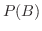 を求めよう.
を求めよう.
2. ある患者がある種の症状を訴えてきた.医師の経験から,同じ年齢層の人がその症状を訴えるとき,約5%の人がガンであることを知っている.一方,ある精密検査によって真のガン患者に対しては85%の陽性反応を示し,ガン患者でない人にも5%の陽性反応を示す.もしある患者がその精密検査の結果陽性反応を示した場合,その患者がガン患者である確率を求めよう.
3. 次の関係を示そう.
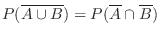
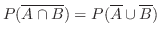
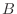 と
と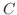 が互いに排反ならば,
が互いに排反ならば,