さいころを投げてどの目が出るか,1枚の硬貨を投げて表がでるか裏が出るかは,実際に投げてみないと分からない.このように,ほぼ一定の条件のもとで,繰り返し起こる現象を観察したり実験することを試行(experiment)という.試行によって起こる結果(outcome)は一般に多数あるが,その起こる事柄を事象(event)という.また,試行によって起こりえるすべての事象の集まりを標本空間(sample space)といい,一般に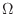 で表す.事象のうち,これ以上簡単なものに分解できないような事象を根元事象(elementary outcomes)という.
で表す.事象のうち,これ以上簡単なものに分解できないような事象を根元事象(elementary outcomes)という.
演習問題 2..1
1. 1個のさいころを6回投げるとき,次の確率を求めよう.
- (a)
- 1の目が1回出る.
- (b)
- 1の目が4回出る.
- (c)
- 1の目が出るのは4回以下である.
- (d)
- 1の目が出るのは5回以上である.
2. 1つの袋に白玉が5個,赤玉が3個,黒玉が2個入っている.その中から4個の球を取り出すとき,次の確率を求めよう.
- (a)
- 全部が白である場合.
- (b)
- 白がちょうど2個である場合.
- (c)
- 白が2個以内.
- (d)
- 白が2個,赤が2個.
- (e)
- 白,赤,黒がともに含まれている場合
3. 1から10までの番号のついたカードがある.これらのカードを勝手に1列に並べるとき,次の確率を求めよう.
- (a)
- 1から10までがその順に並ぶ場合
- (b)
- 4のカードがちょうど4番目にある場合
- (c)
- 1が最初に,4が4番目にある場合
4. 広い方眼紙に縦横に8cm間隔に線を引いて,8cm四方の正方形が沢山かかれているとする.直径が3cmの円板を投げるとき,次の確率を求めよう.
- (a)
- 円板が1つの正方形の中に入る.
- (b)
- 円板が正方形の辺にかかる.
- (c)
- 円板が4つの正方形にまたがる.
5.
4個の白玉と6個の赤玉のはいっている袋がある.この袋から,同時に2個を取り出すとき次の確率を求めよう.
- (a)
- 2個とも白玉である確率
- (b)
- 1個だけ白玉である確率
- (c)
- 少なくとも1個は白玉である確率
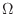 で表す.事象のうち,これ以上簡単なものに分解できないような事象を根元事象(elementary outcomes)という.
で表す.事象のうち,これ以上簡単なものに分解できないような事象を根元事象(elementary outcomes)という.
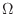 は
は
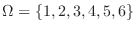 である.ここで,出た目が偶数であるという事象
である.ここで,出た目が偶数であるという事象 を考えると,
を考えると,
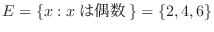 となる.
となる. の根元事象が全部で
の根元事象が全部で 個あり,それらのどれが起こることも同様に確からしいとする.このとき.ある事象
個あり,それらのどれが起こることも同様に確からしいとする.このとき.ある事象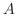 の起こる根元事象が
の起こる根元事象が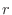 個であるとき,事象
個であるとき,事象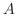 の起こる確率を
の起こる確率を
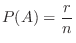
 回おこなったとき,事象
回おこなったとき,事象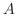 が
が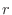 回起こったとする.いま,試行の回数
回起こったとする.いま,試行の回数 を増やしていくとき,相対度数
を増やしていくとき,相対度数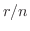 が一定の値
が一定の値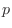 に近づくならば,事象
に近づくならば,事象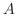 の起こる確率を
の起こる確率を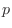 と定義する.これを統計的確率という.
と定義する.これを統計的確率という.