Next: 分布(Chi square distribution) Up: 標本分布 Previous: 標本分布 目次
 の無作為標本
の無作為標本
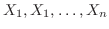 とするとき,各変数は母集団の分布と同じ分布に従う確率変数と考えられる. これを標本確率変数(Sample random variable)とよぶ。ここで,母平均値(population mean)
とするとき,各変数は母集団の分布と同じ分布に従う確率変数と考えられる. これを標本確率変数(Sample random variable)とよぶ。ここで,母平均値(population mean)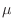 ,母分散(population variance)
,母分散(population variance)
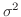 が存在するものとすると,標本確率変数
が存在するものとすると,標本確率変数
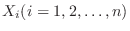 は互いに独立に母集団に従う。よって,
は互いに独立に母集団に従う。よって,
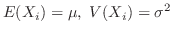
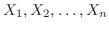 を用いて母平均と母分散を推定することを考える。
を用いて母平均と母分散を推定することを考える。
まず,素朴に考えて,
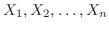 を
を 個のデータの集まりとして,その平均と分散を求めると,
個のデータの集まりとして,その平均と分散を求めると,
|
|
標本平均 |
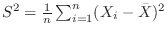 , , |
標本分散 |
となる。
1.
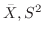 は母平均
は母平均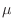 , 母分散
, 母分散
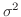 を推測するのに適当な統計量だろうか。ここで,統計量とは標本確率変数
を推測するのに適当な統計量だろうか。ここで,統計量とは標本確率変数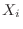 の関数のことである。
の関数のことである。