Next: 標本分布 Up: 理論分布 Previous: 指数分布(Exponential distribution) 目次
 の確率密度関数が
の確率密度関数が
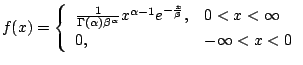
で与えられるとき,確率変数はガンマ分布(Gamma distribution)に従うといい,
![]() で表します.ここで,
で表します.ここで,
ガンマ関数の特徴
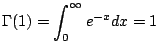
式(4.1)の両辺を
![]() で割ると,
で割ると,
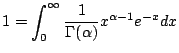
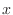 を
を
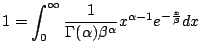
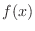 とおくと,ガンマ関数の定義が得られる.また,この式より,ガンマ関数は確率密度関数であることも分かる.
とおくと,ガンマ関数の定義が得られる.また,この式より,ガンマ関数は確率密度関数であることも分かる.
1. あるガスステイションで1週間に売れるガソリンの量 キロリットルは,次の密度関数をもつ分布に従っているとする.
キロリットルは,次の密度関数をもつ分布に従っているとする.
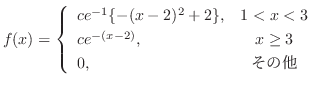
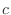 の値を定めよ.
の値を定めよ.
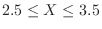 となる確率を求めよ.
となる確率を求めよ.
2. 日本人の血液型はA型 35%,B型 25%,AB型 10%,O型 30%であるといわれている.いま,4人いたとき,4人とも血液型が異なる確率を求めよ.
3.. 電話での通話時間は平均2分の指数分布に従うとする.電話ボックスにすでに話し中の人も含めて3人いたとき,10分以上待たなければならない確率を求めよ.