Next: ガンマ分布(Gamma distribution) Up: 理論分布 Previous: 超幾何分布(Hypergeometric distribution) 目次
 の確率密度関数が
の確率密度関数が
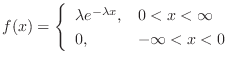
で与えられるとき,確率変数は指数分布(Exponential distribution)に従うといい,
![]() で表します.ここで,
で表します.ここで,
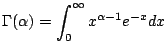
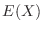 |
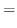 |
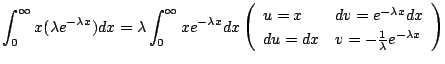 |
|
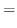 |
![$\displaystyle \lambda\left[-\frac{1}{\lambda}xe^{-\lambda x} + \frac{1}{\lambda^{2}}e^{-\lambda x}\right]_{0}^{\infty}$](img28.gif) |
||
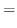 |
分散は母関数を用いて求める.
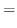 |
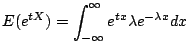 |
||
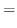 |
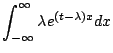 |
||
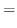 |
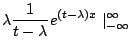 |
||
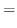 |
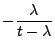 |
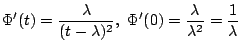
II. ある人の通話時間 は平均3分の指数分布に従うものとする.
は平均3分の指数分布に従うものとする.
(a) その人の通話が4分以内に終わる確率を求めよ.
(b) また,その人が通話をはじめてから2分が経過しているとき,その後4分以内に終わる確率を求めよ.