Next: 行列の基本変形 Up: 行列と行列式 Previous: 行列と行列式 目次 索引
1.
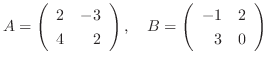 について, 次の式を計算せよ.
について, 次の式を計算せよ.
2.
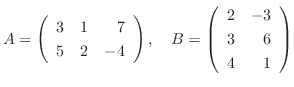 のとき,
のとき, 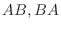 を求めよ.
を求めよ.
3.
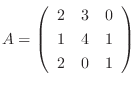 のとき,
のとき,
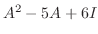 を計算せよ.
を計算せよ.
4.  と
と 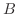 が
が 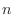 次の対称行列のとき,
次の対称行列のとき, 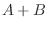 は対称行列であることを示せ.
は対称行列であることを示せ.
5.  と
と 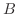 が
が 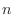 次の対称行列のとき,
次の対称行列のとき, 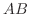 はいつも対称行列か調べ,
はいつも対称行列か調べ, 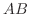 がいつも対称行列になるための必要十分条件を求めよ.
がいつも対称行列になるための必要十分条件を求めよ.
6.  が交代行列ならば,
が交代行列ならば, 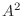 は対称行列であることを示せ.
は対称行列であることを示せ.
7. 行列
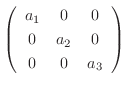 との積が交換可能な行列をすべて求めよ.ただし,
との積が交換可能な行列をすべて求めよ.ただし,
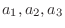 は相異なる実数とする.
は相異なる実数とする.
8. 正方行列  は, 対称行列と交代行列の和として一意的に表せることを証明せよ.
は, 対称行列と交代行列の和として一意的に表せることを証明せよ.
9.
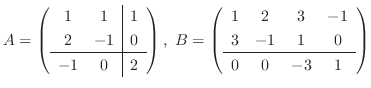 の積を求めよ.
の積を求めよ.