Next: 行列の対角化 Up: 線形写像 Previous: 線形写像 目次 索引
1.
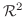 の基底
の基底
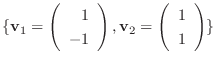 から一般の基底
から一般の基底
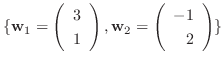 への変換行列
への変換行列 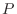 を求めよ.
を求めよ.
2. 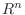 の基底
の基底
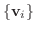 から
から
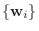 への変換行列
への変換行列 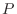 は
は 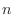 次の正則行列であることを示せ.
次の正則行列であることを示せ.
3. 次の行列の固有値と固有空間を求めよ.
4. 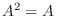 を満たす
を満たす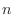 次の正方行列
次の正方行列  の固有値を求めよ.
の固有値を求めよ.
5. 行列  の固有値を
の固有値を
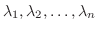 とすると,
とすると, 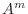 の固有値は
の固有値は
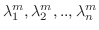 であることを証明せよ.
であることを証明せよ.
6.
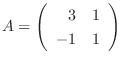 とするとき, ケイリー・ハミルトンの定理をもちいて
とするとき, ケイリー・ハミルトンの定理をもちいて
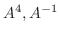 を求めよ.
を求めよ.
7. 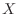 を2次の行列とするとき,
を2次の行列とするとき,
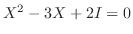 を満たす
を満たす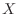 をすべて求めよ.
をすべて求めよ.