Next: 行列の変換と固有値 Up: 線形写像 Previous: 線形写像 目次 索引
1. 次の写像のうち線形写像はどちらか.
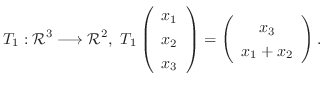
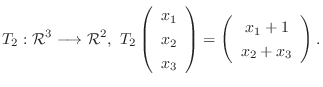
2. 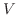 は
は 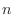 次元ベクトル空間,
次元ベクトル空間,
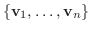 を
を 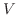 の基底とする.
の基底とする.
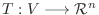 を
を
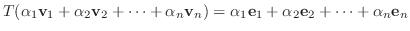 と定義すると,
と定義すると, 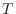 は線形写像になることを示せ.
は線形写像になることを示せ.
3. 線形写像
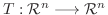 について, 次の条件は同値であることを証明せよ.
について, 次の条件は同値であることを証明せよ.
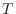 は同型写像である.
は同型写像である.
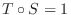 を満たす線形写像
を満たす線形写像
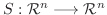 が存在する.
が存在する.
4.
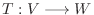 が線形写像のとき,
が線形写像のとき,
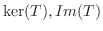 は
は 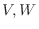 の部分空間であることを示せ.
の部分空間であることを示せ.
5.
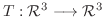 が
が
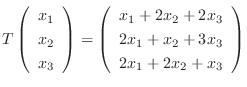 のとき, 標準基底
のとき, 標準基底
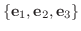 に関する
に関する 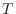 の行列表現
の行列表現![$[T]$](img137.png) と基底
と基底
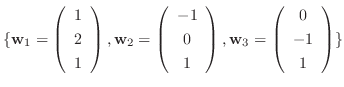 に関する行列表現
に関する行列表現
![$[T]_{\bf w}$](img139.png) を求めよ.
を求めよ.
また
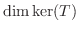 を求めよ.
を求めよ.
6.
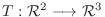 が,
が,
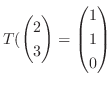 ,
,
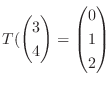 をみたすとき,
をみたすとき,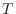 の行列表現を求めよ.
の行列表現を求めよ.