next up previous contents index
Next: 行列の分解 Up: 行列と行列式 Previous: 行列の基本変形   目次   索引

連立1次方程式と逆行列

演習問題2-6

1. 次の連立1次方程式をガウスの消去法を用いて解け．

(a) $\left\{\begin{array}{rrr} x-3y&=&5\\ 3x-5y&=&7 \end{array}\right . $

(b) $\left\{\begin{array}{rrr} x+y+z&=&3\\ x+2y+2z&=&5\\ x+2y+3z&=&6 \end{array}\right . $

(c) $\left\{\begin{array}{rrr} x_{1}+x_{2}+x_{3}+x_{4}&=&1\\ x_{1}+2x_{2}+3x_{3}+4x_{4}&=&2\\ x_{1}+4x_{2}+9x_{3}+16x_{4}&=&6 \end{array}\right .$

2. 次の連立1次方程式が解をもつように, 定数 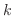$k$ の値を定めよ．また, そのときの解を求めよ．
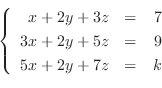
\begin{displaymath}\begin{array}{l} \left\{\begin{array}{rrr} x+2y+3z&=&7\\ 3x+2y+5z&=&9\\ 5x+2y+7z&=&k \end{array}\right . \end{array}\end{displaymath}

3. 次の行列の正則性を判定し, 正則ならば逆行列を求めよ．

(a) $\left(\begin{array}{rrr} 2&3&4\\ 1&2&3\\ -1&1&4 \end{array}\right)$

(b) $\left(\begin{array}{rrrr} 0&0&0&1\\ 0&0&1&0\\ 0&1&0&0\\ 1&0&0&0 \end{array}\right)$

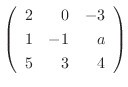4. $\left(\begin{array}{rrr} 2&0&-3\\ 1&-1&a\\ 5&3&4 \end{array}\right)$ が正則行列となるのは 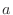$a$ がどのようなときか調べよ．

5. 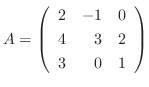$A = \left(\begin{array}{rrr} 2&-1&0\\ 4&3&2\\ 3&0&1 \end{array}\right)$ は正則行列であることを示し, $A$ を基本行列の積で表せ．

6. 正方行列のひとつの行の成分がすべて 0 ならば, $A$ は正則でないことを証明せよ．

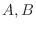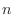7. $A,B$ がともに $n$ 次正則行列ならば, 積 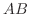$AB$も正則で,

$\displaystyle (AB)^{-1} = B^{-1}A^{-1} $

となることを証明せよ．