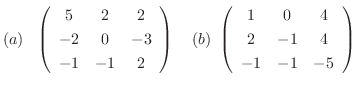Next: 問題解答 Up: Jordan標準形 Previous: ベキ零行列の標準形 目次 索引
 Jordanブロック
Jordanブロック

次の形をした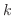 次正方行列を, 複素数
次正方行列を, 複素数 に対する
に対する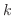 次のJordanブロック (Jordan block)またはJordan細胞いう.
次のJordanブロック (Jordan block)またはJordan細胞いう.
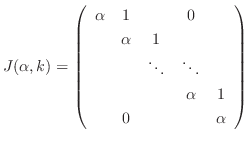
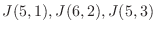
解
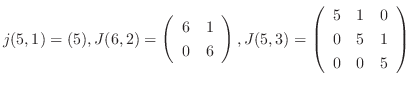
いくつかのJordanブロックを対角線に沿って並べて得られる行列
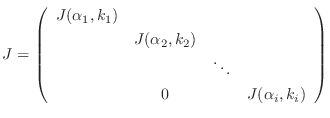
 ベキ零行列の標準形
ベキ零行列の標準形

任意の 次正方行列
次正方行列  は適当な正則行列
は適当な正則行列  をとり
をとり 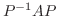 をJordan行列にできるでしょうか.まず,
をJordan行列にできるでしょうか.まず,  がベキ零行列の場合を考えてみましょう.
がベキ零行列の場合を考えてみましょう.
行列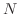 をベキ零行列とすると, ベキ零行列の定義より
をベキ零行列とすると, ベキ零行列の定義より
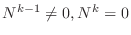 となる整数
となる整数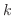 が存在します.ここで
が存在します.ここで
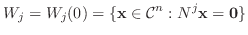
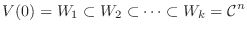
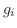 |
 |
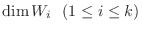 |
|
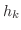 |
 |
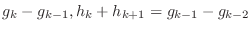 |
|
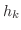 |
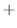 |
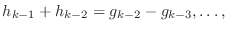 |
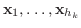 を
を 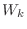 に属する1次独立なベクトルで
に属する1次独立なベクトルで
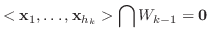
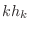 個のベクトル
個のベクトル
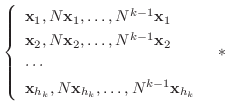
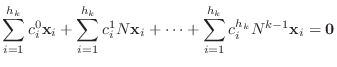
![$N^{[k-1]}$](img1573.png) をかけると, 第2項以下の和は0となり
をかけると, 第2項以下の和は0となり
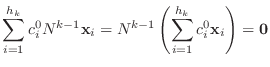
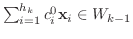 となりますが, 仮定
となりますが, 仮定
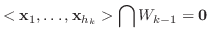
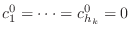 でなければなりません.以下同様にこの手続きを繰り返せば,
でなければなりません.以下同様にこの手続きを繰り返せば,
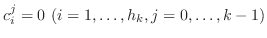 を得ます.
を得ます.
次に, 以下の条件を満たすベクトル
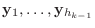 を考えます.
を考えます.
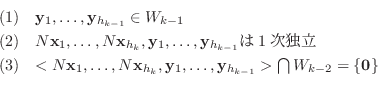
このとき次の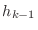 個のベクトルと(*)のベクトルを合わせたものも1次独立となります.
個のベクトルと(*)のベクトルを合わせたものも1次独立となります.
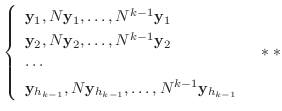
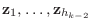 を考えます.
を考えます.
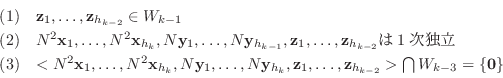
以下この議論を繰り返すことができ, 最終的に次のベクトル全体は
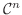 の基底になります.
の基底になります.
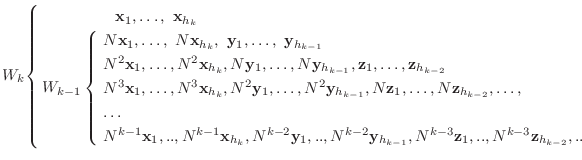
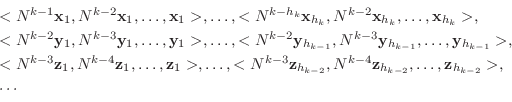
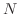 -不変となります.そこで,
-不変となります.そこで, 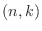 行列
行列
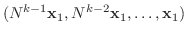 に
に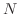 を左からかけると
を左からかけると
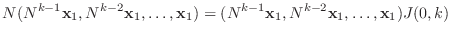
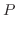 |
 |
 |
|
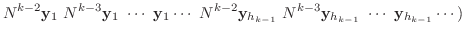 |
 は正則行列になり
は正則行列になり
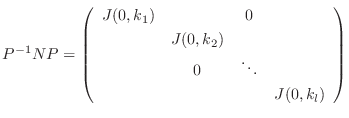
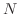 のJordan標準形(Jordan canonical form)いいます.ここまでをまとめると次の定理を得ます.
のJordan標準形(Jordan canonical form)いいます.ここまでをまとめると次の定理を得ます.
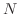 を
を 次の正方行列とする.このとき適当な正則行列
次の正方行列とする.このとき適当な正則行列 により
により
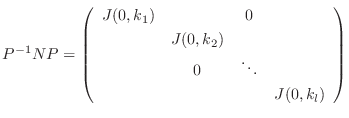
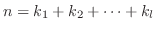 である.
である.
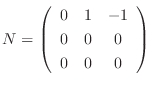
解 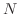 は
は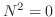 を満たすので, 指数2のベキ零行列である.
よって,
を満たすので, 指数2のベキ零行列である.
よって, 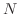 の固有値は0だけであり, 固有値0に対する広義固有空間
の固有値は0だけであり, 固有値0に対する広義固有空間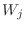 を考える.
を考える.
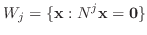
 である.
である.
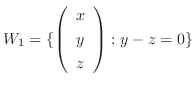
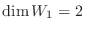 .そこで, 例えば,
.そこで, 例えば,
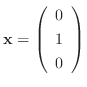 をとると
をとると
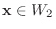 ,
,
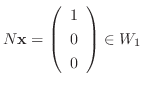
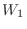 は2次元であるから
は2次元であるから
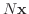 と1次独立なベクトル
と1次独立なベクトル
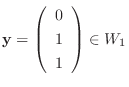 がとれる.このとき
がとれる.このとき
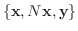 は
は
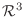 の基底である.
の基底である.
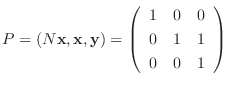
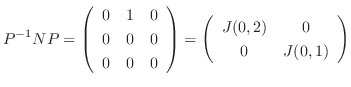
 Jordan標準形
Jordan標準形

 を
を 次の正方行列, その固有多項式を
次の正方行列, その固有多項式を
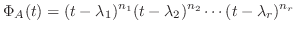
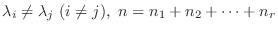
 により
により
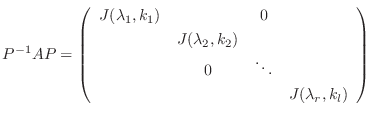
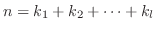 である.
である.
証明
固有値
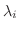 の広義固有空間
の広義固有空間
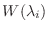 に対して, 部分空間の列
に対して, 部分空間の列
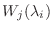 |
 |
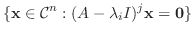 |
|
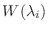 |
 |
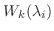 |
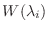 は
は
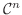 の
の -不変および
-不変および
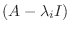 -不変な部分空間になる.よって, 定理5.2の議論を行列
-不変な部分空間になる.よって, 定理5.2の議論を行列
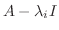 と部分空間の列(5.2)に対して適用できる.
と部分空間の列(5.2)に対して適用できる.
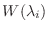 の基底
の基底
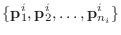
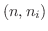 行列
行列
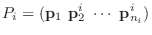
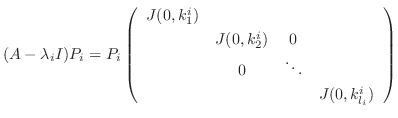
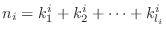 の形になるものを選ぶことができる.ここで,
の形になるものを選ぶことができる.ここで,
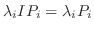 を右辺に移項すると
を右辺に移項すると
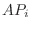 |
 |
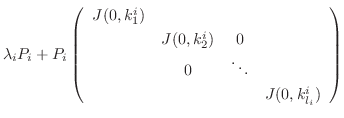 |
|
 |
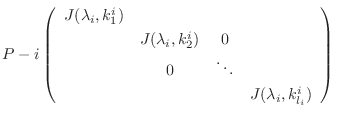 |
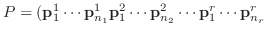
 は正則行列となり
は正則行列となり
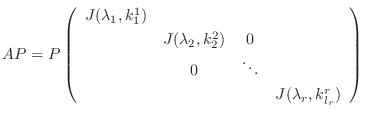
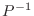 をかけると, 求めるJordan行列
をかけると, 求めるJordan行列
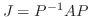 を得る.
を得る.

 も求めよう.
も求めよう.
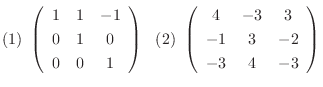
解
(1)
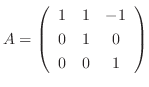 の固有値を求めると
の固有値を求めると
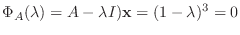
 の固有値は1だけである.よって,
の固有値は1だけである.よって, 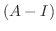 はベキ零行列なるので, 例題5.2より,
はベキ零行列なるので, 例題5.2より,
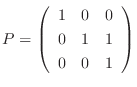
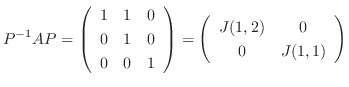
(2)
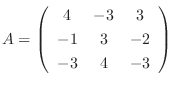 の固有値を求めると
の固有値を求めると
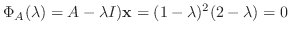
 の固有値は1と2である.固有値1に対して
の固有値は1と2である.固有値1に対して
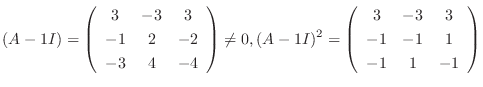
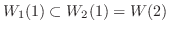
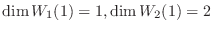
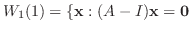
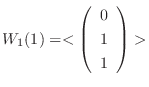
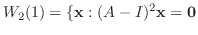
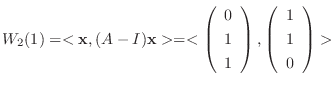
次に, 固有値2に対して
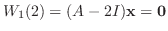
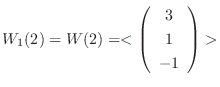
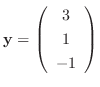 をとる.
をとる.
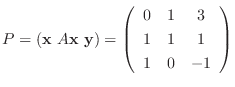
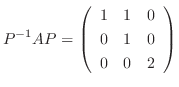
 のJordan標準形である.
のJordan標準形である.
1. 次のベキ零行列の標準形と変換行列 を求めよう.
を求めよう.
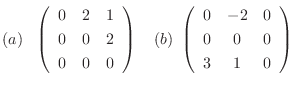
 を求めよう.
を求めよう.