Scalar triple product

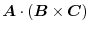$\boldsymbol{A}\cdot(\boldsymbol{B}\times\boldsymbol{C})$ is called Scalar triple product and can be solved by

$$(A_{1}\:\boldsymbol{i} + A_{2}\:\boldsymbol{j} + A_{3}\:\boldsymb... ...A_{2}&A_{3}\\ B_{1}&B_{2}&B_{3}\\ C_{1}&C_{2}&C_{3} \end{array}\right\vert .$$

．

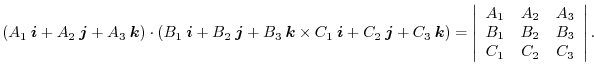
Vectors 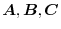$\boldsymbol{A}, \boldsymbol{B}, \boldsymbol{C}$ are on the same plane, then we say 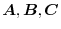$\boldsymbol{A}, \boldsymbol{B}, \boldsymbol{C}$はcoplanar or linearly dependent. Also，if 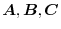$\boldsymbol{A}, \boldsymbol{B}, \boldsymbol{C}$ are not on the same plane, we say not coplanar or linearly independent．

The absolute value of the scalar triple product can be thought of as the volume of a parallelepiped made up of 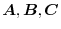$\boldsymbol{A}, \boldsymbol{B}, \boldsymbol{C}$. Then to check to see whether three vectors 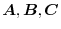$\boldsymbol{A}, \boldsymbol{B}, \boldsymbol{C}$ are on the same plane or not, we can use the scalar triple product.

Theorem 1..2  

Vectors $\boldsymbol{A}, \boldsymbol{B}, \boldsymbol{C}$ are coplanar if and only if the scalar triple product $\boldsymbol{A}\cdot(\boldsymbol{B}\times\boldsymbol{C}) = 0$．

Example 1..4  

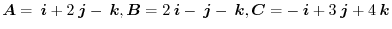Show that $\boldsymbol{A} = \:\boldsymbol{i} + 2\:\boldsymbol{j} - \:\boldsymbol{k}, \bold... ...{k}, \boldsymbol{C} = -\:\boldsymbol{i} + 3\:\boldsymbol{j} + 4\:\boldsymbol{k}$ is not coplanar.

Answer 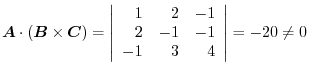$\boldsymbol{A}\cdot(\boldsymbol{B}\times\boldsymbol{C}) = \left\vert\begin{arra... ...}1 & 2 & -1\\ 2 & -1 & -1\\ -1 & 3 & 4 \end{array}\right\vert = -20 \neq 0$．Thus they are not coplanar．

Question 1..8  

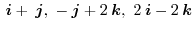Check to see $\:\boldsymbol{i} + \:\boldsymbol{j},\ -\:\boldsymbol{j} + 2\:\boldsymbol{k},\ 2\:\boldsymbol{i} - 2\:\boldsymbol{k}$ is coplanar or not．