Next: Scalar triple product Up: Application of inner product Previous: Application of inner product Contents Index
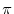 is specified as its front and the other side of the front is back, the front and back can be specified for this plane
is specified as its front and the other side of the front is back, the front and back can be specified for this plane 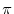 . A plane whose front and back are specified in this way is called a directed plane. To display the orientation of the directed plane, consider a shape on the directed plane
. A plane whose front and back are specified in this way is called a directed plane. To display the orientation of the directed plane, consider a shape on the directed plane 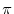 , and when you turn the edge of the shape so that you see this shape on your left shoulder, it is perpendicular to this plane and the right-hand thread the direction of travel represents the front and back of the directed plane. A vector of magnitude 1 perpendicular to this plane and in the direction of the right-handed screw is called a unit normal vector, andit is represented by a
, and when you turn the edge of the shape so that you see this shape on your left shoulder, it is perpendicular to this plane and the right-hand thread the direction of travel represents the front and back of the directed plane. A vector of magnitude 1 perpendicular to this plane and in the direction of the right-handed screw is called a unit normal vector, andit is represented by a
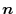 .
.
![\includegraphics[width=6cm]{VECANALFIG/areavec.eps}](img61.png)
When the area of?the figure on this directed plane 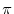 is
is  , the vector
, the vector
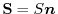 is called the area vector of this figure. From
is called the area vector of this figure. From
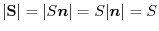 , the size of the area vector represents the area of this figure, The direction of
, the size of the area vector represents the area of this figure, The direction of 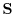 represents the slope of this figure in space.
represents the slope of this figure in space.
![\includegraphics[width=5cm]{VECANALFIG/volvec.eps}](img66.png)
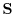 be the bottom, and the volume of the pillar with the generatrix parallel to the vector
be the bottom, and the volume of the pillar with the generatrix parallel to the vector
 be
be 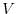 . At this time, assume that the angle between
. At this time, assume that the angle between
 and
and 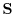 is an acute angle. At this time, it is assumed that the angle between
is an acute angle. At this time, it is assumed that the angle between
 and
and 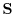 is an acute angle. Then, the height
is an acute angle. Then, the height 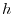 of this pillar is expressed as
of this pillar is expressed as
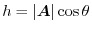
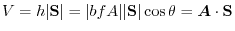
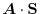 directed volume.
directed volume.
![\includegraphics[width=6cm]{VECANALFIG/dirarea.eps}](img72.png)
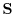 and a directed plane
and a directed plane 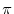 , as shown in the figure above. At this time, the image obtained by projecting the rectangle ABCD onto the directed plane
, as shown in the figure above. At this time, the image obtained by projecting the rectangle ABCD onto the directed plane 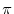 is A'B'C'D'. Find the area of ??the rectangle A'B'C'D'when the angle between the rectangle ABCD and the directed plane
is A'B'C'D'. Find the area of ??the rectangle A'B'C'D'when the angle between the rectangle ABCD and the directed plane 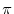 is
is 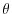 ..
First, notice that the angle between the area vector
..
First, notice that the angle between the area vector 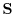 and the normal vector
and the normal vector
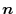 of the directed plane
of the directed plane 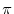 is
is 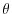 . Then, the area
. Then, the area  of the rectangle A'B'C'D'is
of the rectangle A'B'C'D'is
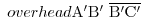 .Also,
.Also,
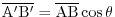 ,
,
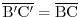 .Therefore,
.Therefore,
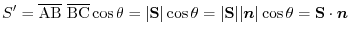
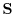 and a directed plane
and a directed plane 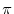 , this plane figure is obtained by projecting it onto the plane
, this plane figure is obtained by projecting it onto the plane 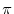 . The area of ?the figure
. The area of ?the figure  is given by
is given by
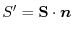
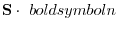 is called the bf directed area of the orthodox projection on the directed plane
is called the bf directed area of the orthodox projection on the directed plane 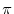 of this plane.
of this plane.