Next: Differentiation / integration of Up: Application of inner product Previous: Scalar triple product Contents Index
The product of three vectors
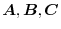
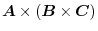 is called vector triple product and the following formula holds..
is called vector triple product and the following formula holds..
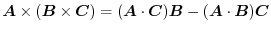
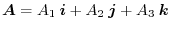 ,
,
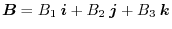 ,
,
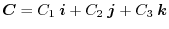 . Then,
. Then,
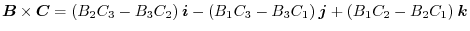
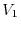 of
of
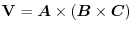 is
is
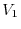 |
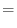 |
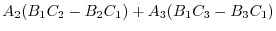 |
|
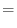 |
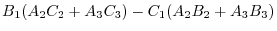 |
||
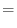 |
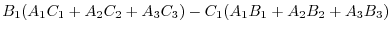 |
||
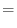 |
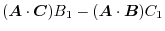 |
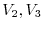 .
.
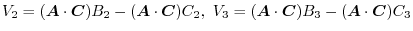
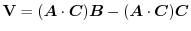
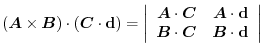 .
.
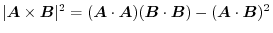 .
.