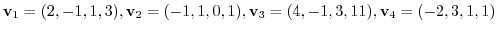Elementary Row Operation

Exercise2-4

1. Find the row reduced matrix which is row equivalent to $A = \left(\begin{array}{rrrr} 1&-2&3&-1\\ 2&-1&2&2\\ 3&0&2&3 \end{array}\right)$ ．

2. Find the rank of the following matrices．

(a) $\left(\begin{array}{rrrr} 2&4&1&-2\\ -3&-6&2&-4 \end{array}\right)$

(b) $\left(\begin{array}{rrr} 2&-1&3\\ 1&2&-3\\ 3&-4&9 \end{array}\right)$

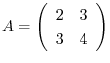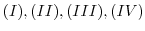3. Given $A = \left(\begin{array}{cc} 2&3\\ 3&4 \end{array}\right)$ . Apply elmentary operations $(I),(II),(III),(IV)$ ．

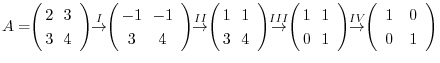
$\displaystyle A = \!\! \left(\begin{array}{cc} \!\!2&\!\!3\\ \!\!3&\!\!4 \end{... ...el{IV}{\rightarrow} \!\! \left(\begin{array}{cc} 1&0\\ 0&1 \end{array}\right)$

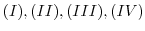Find the elementary matrices of $(I),(II),(III),(IV)$

. Show the matrix 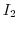$I_{2}$ as a product of the matrix $A$

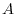and elementary matrices．

4. 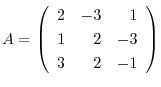$A = \left(\begin{array}{rrr} 2&-3&1\\ 1&2&-3\\ 3&2&-1 \end{array}\right)$ can be reduced to the identiry matrix by using the elementary row operation．Find the product of matrices 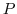$P$ so that $PA = I$ .

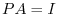5. Find the dimension of the subspace spanned by the following vectors.

$\displaystyle {\bf v}_{1} = (2,-1,1,3), {\bf v}_{2} = (-1,1,0,1), {\bf v}_{3} = (4,-1,3,11), {\bf v}_{4} = (-2,3,1,1)$