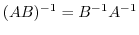System of linear equations and Inverse matrix

Exercise2-6

1. Solve the following system of linear equations using Gaussian elimination．

(a) $\left\{\begin{array}{rrr} x-3y&=&5\\ 3x-5y&=&7 \end{array}\right .$

(b) $\left\{\begin{array}{rrr} x+y+z&=&3\\ x+2y+2z&=&5\\ x+2y+3z&=&6 \end{array}\right .$

(c) $\left\{\begin{array}{rrr} x_{1}+x_{2}+x_{3}+x_{4}&=&1\\ x_{1}+2x_{2}+3x_{3}+4x_{4}&=&2\\ x_{1}+4x_{2}+9x_{3}+16x_{4}&=&6 \end{array}\right .$

2. Determine the value of 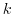$k$ so that the following system of linear equations has a solution.
$$\begin{array}{l} \left\{\begin{array}{rrr} x+2y+3z&=&7\\ 3x+2y+5z&=&9\\ 5x+2y+7z&=&k \end{array}\right . \end{array}$$

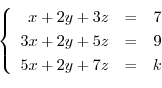
3. Determine whether the following matrix is regular. If so, find the inverse matrix, (a) $\left(\begin{array}{rrr} 2&3&4\\ 1&2&3\\ -1&1&4 \end{array}\right)$

(b) $\left(\begin{array}{rrrr} 0&0&0&1\\ 0&0&1&0\\ 0&1&0&0\\ 1&0&0&0 \end{array}\right)$

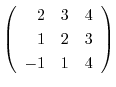
4. Determine the value 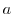$a$ so that the following matrix is regular.

$\left(\begin{array}{rrr} 2&0&-3\\ 1&-1&a\\ 5&3&4 \end{array}\right)$

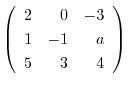
5. Show that the following matrix is regular, and show the following matrix as a product of elementary matrices. $A = \left(\begin{array}{rrr} 2&-1&0\\ 4&3&2\\ 3&0&1 \end{array}\right)$．

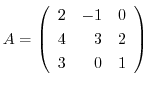6. Suppose that all entries of one row of the square matrix are 0. The show that 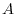$A$ is not regular.

7. Suppose that 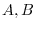$A,B$ are regular matrices of the order 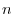$n$. Then show thatthe product of 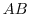$AB$ is also regular and satisfies

$$(AB)^{-1} = B^{-1}A^{-1}$$