Next: Elementary Row Operation Up: Matrices and Determinant Previous: Matrices and Determinant 目次 索引
1. For matrices
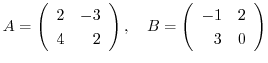 , evaluate the followings:
, evaluate the followings:
2. For matrices
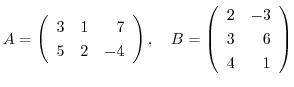 , find
, find 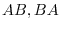 .
.
3. For the matrix
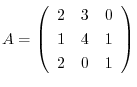 , calculate
, calculate
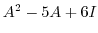 .
.
4. Let 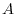 and
and 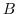 be symmetric matrices of the order
be symmetric matrices of the order 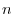 . Show that
. Show that 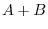 is a symmetric matrix.
is a symmetric matrix.
5. Let 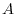 and
and 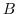 be symmetric matrices of the order
be symmetric matrices of the order 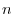 . Find the necessary and sufficient conditions so that
. Find the necessary and sufficient conditions so that 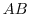 is a symmetric matrix.
is a symmetric matrix.
6. Suppose that 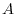 is a skew symmetric matrix. Then show that
is a skew symmetric matrix. Then show that 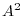 is a symmetric marix.
is a symmetric marix.
7. Find matrices so that the product of
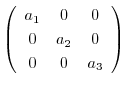 is interchangeable.Here,
is interchangeable.Here,
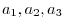 are different real numbers.
are different real numbers.
8. Show that any square matrix 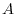 can be expressed by the sum of a symmetric matrix and a skew symmetric matrix.
can be expressed by the sum of a symmetric matrix and a skew symmetric matrix.
9. Find the product of 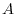 and
and 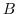 , where
, where
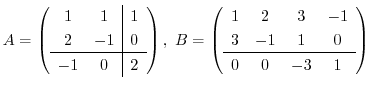 .
.