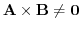Linearly independent and linearly dependent

Exercise1-6

1. For vectors 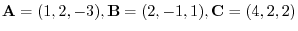${\bf A} = (1,2,-3), {\bf B} = (2,-1,1), {\bf C} = (4,2,2)$ , find the followings:

(a) ${\bf A}\times{\bf B}$ (b) ${\bf C}\times({\bf A}\times{\bf B})$ (c) ${\bf C}\cdot({\bf A}\times{\bf B})$

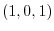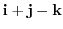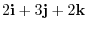2. Find the equation of the plane going thru a point $(1,0,1)$ and parallel to the plane with the vector ${\bf i} + {\bf j} - {\bf k}$ and $2{\bf i} + 3{\bf j} + 2{\bf k}$ for sides.

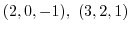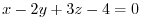3. Find the equation of the plane going thru $(2,0,-1), \ (3,2,1)$ and perpendicular to the plane $x - 2y + 3z - 4 = 0$ ．

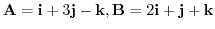4. Find the area of the triangle whose sides are given by ${\bf A} = {\bf i} + 3{\bf j} - {\bf k}, {\bf B} = 2{\bf i} + {\bf j} + {\bf k}$ .．

5. Find the moment vector of 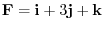${\bf F} = {\bf i} + 3{\bf j} + {\bf k}$ around the point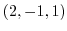 $(2,-1,1)$

6. The volume of the parallelogram composed by the vectors A,B,C is the same as the absolute value of

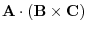
$\displaystyle {\bf A}\cdot({\bf B}\times{\bf C})$

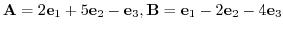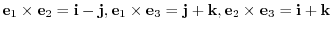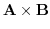7. Given ${\bf A} = 2{\bf e}_{1} + 5{\bf e}_{2} - {\bf e}_{3}, {\bf B} = {\bf e}_{1} - 2{\bf e}_{2} - 4{\bf e}_{3}$ and ${\bf e}_{1}\times{\bf e}_{2} = {\bf i} - {\bf j}, {\bf e}_{1}\times{\bf e}_{3} = {\bf j} + {\bf k},{\bf e}_{2}\times{\bf e}_{3} = {\bf i} + {\bf k}$ . Find ${\bf A}\times{\bf B}$ ．

8. Determine whether 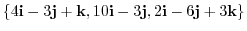$\{4{\bf i} - 3{\bf j} + {\bf k}, 10{\bf i} - 3{\bf j}, 2{\bf i} -6{\bf j} + 3{\bf k}\}$ is linearly independent or not.

9. Show the following functions are linearly independent on any interval 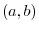$(a,b)$

(a) $\{1, x, x^2\}$ (b) $\{\sin{x}, \cos{x}\}$

10. Show that geometric vectors A, B is linearly independent if and only if ${\bf A} \times {\bf B} \neq {\bf0}$