Subspace and Dimension

Exercise1-8

1. Determine whether 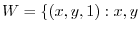$W = \{(x,y,1) : x,y$   real$\}$ is a subspace of the vector space $R^3$．

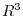2. Show that 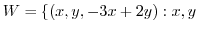$W = \{(x,y,-3x+2y) : x, y$   real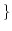$\}$ is a subspace of the vector space $R^3$.

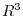3. Find the basis of a vector space 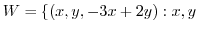$W = \{(x,y,-3x+2y) : x, y$   real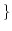$\}$ ．Find the dimension of $W$．

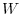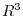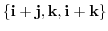
4. Show the following set of vectors is a basis of the vector space $R^3$．

$$\{{\bf i} + {\bf j} , {\bf k} , {\bf i } + {\bf k}\}$$

5. Find the dimension of the following subspace．

$$\{3, x-2, x+3, x^2+1\}$$

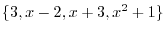
6. From the vectors 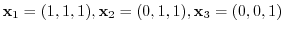${\mathbf x}_{1} = (1,1,1), {\mathbf x}_{2} = (0,1,1), {\mathbf x}_{3} = (0,0,1)$ , create an orthonormal system.

7. Let 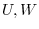$U,W$ be subspace of a vector space 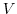$V$. Show the following dimensional equation holds.

$$\dim (U + W) = \dim U + \dim W - \dim(U \cap W).$$

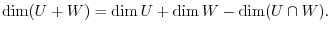
8. Show that any set of vectors with more than 4 vectors in 3D vector spaceis linearly dependent.