Next: Linearly independent and linearly Up: Vector Space Previous: Geometric vectors and vector 目次 索引
1. For vectors
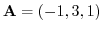 and
and
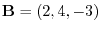 , find the followings:
(a)
, find the followings:
(a)
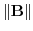 (b)
(b)
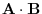 (c) Angle between A and B
(d) Unit vector in the dierction of A
(c) Angle between A and B
(d) Unit vector in the dierction of A
2. Determine which system is orthogonal. If it is orthogonal, find the orthonormal system.
3. Find an equation of plane going thru a point 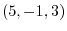 and normal vector is 2i + j - k.
and normal vector is 2i + j - k.
4. Let A,B be space vectors. Then prove the following inequality:
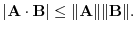
5. LetA, B, C be space vectors. Then show the following inequality:
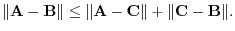
6. Let 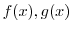 be a function vector in
be a function vector in ![$PC[a,b]$](img29.png) .Show the following:
.Show the following:
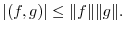
7. For ![$PC[0,2]$](img31.png) , Find the norm of the followings:.
, Find the norm of the followings:.
8. Next three polynomials are called Legendre polynomial.
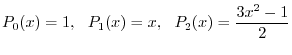
![$PC[-1,1]$](img36.png) .
.